Для такой точности достаточно принять pi = 22/7;
тогда радиус R = корень(4*7/22) = корень(14/11);
(приближенно это 1,12815214963553, а если взять pi = 3,14159265358979, получится 1,12837916709551, то есть разница в ЧЕТВЕРТОМ знаке после запятой.)
Но все равно есть вопрос - а как без калькулятора найти этот корень(14/11), хотя бы с точностью до 1/10?
Вряд ли вы знакомы с такими формулами, но на самом деле это выглядит так
корень(14/11) = корень(1 + 3/11) = (приближенно, если считать, что 3/11 очень мала по сравнению с 1) = 1 + (1/2)*3/11 = 1,136364... это точность, заявленная в задаче, причем я нигде не воспользовался калькулятором (кроме комментариев, конечно)
Между прочим, доказать, что корень(1+x) =(приблизительно) = 1+х/2 очень просто - достаточно возвести в квадрат, получим (1 + х) = (1 + х + x^2/4) если x<<1, то разница совсем не велика. При x = 3/11; x^2/4 < 3/100;
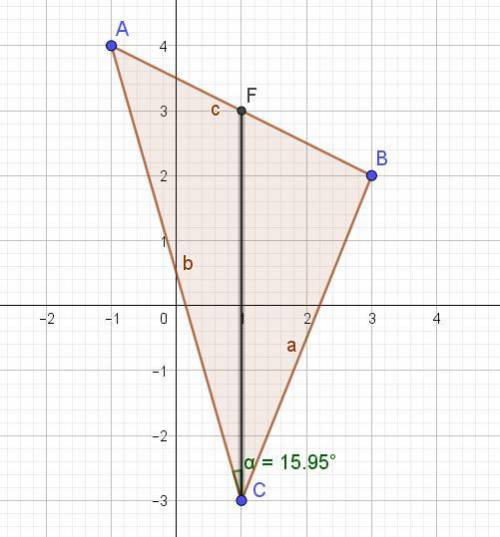
Найдем координату точки F. F- точка , которая делит пополам сторону АВ ( так как CF - медиана).
F = ( (Xa+Xb)/2 ; (Ya+Yb)/2) = ((-1+3)/2 ; (4+2)/2)= (1;3).
Вектор CF = (1-1; 3-(-3)) = (0; 6).
Уравнение медианы CF: (x - 1)/0 = (y - 4)/6.
Получаем общее уравнение CF: 6x - 6 = 0 или х - 1 = 0.
Находим уравнение стороны АС.
Вектор АС = (1-(-1); -3-4) = (2; -7).
Уравнение АС: (x + 1)/2 = (y - 4)/(-7) или в общем виде 7x + 2y - 1 = 0.
Находим угол α между прямыми АС и CF.
cos α = (1*7 + 0*2)/(1*√53) = 7√53/53.
Угол α = 15,9454°.
ответ: ∡ACF=arccos(3*√5/10)
Объяснение:
1. Найдем координату точки F. F- точка , которая делит пополам сторону АВ ( так как CF - медиана)
F = ( (Xa+Xb)/2 ; (Ya+Yb)/2) = ((-1+3)/2 ; (4+2)/2)= (1;3)
2. Найдем длину медианы CF:
CF=sqrt( (Xf-Xc)²+(Yf-Yc)²)= sqrt((1-1)²+ (3-(-3))²)=sqrt(0+9)=3
3. Найдем AF =sqrt ((Xf-Xa)² +(Yf-Ya)²)= sqrt ((1-(-1))²+(3-4)²)= sqrt(2²+1²)=√5
4. Найдем АС=sqrt((Xc-Xa)²+(Yc-Ya)²)=sqrt((1-(-1))²+(-3-(-4))²)=sqrt(2²+1²)=√5
=> ΔACF- равнобедренный (AС=AF).
=>cos ∡ACF= 3/√5/2=3*√5/10
∡ACF=arccos(3*√5/10)
Площадь круга равна S = πR².
По условию S = 4см²,
Известно, что π ≈ 3,1416, тогда
πR² = 4
R = √4/π = √4/3,1416 ≈ 1,128
ответ: R = 1,1см