Правильная четырёхугольная пирамида.
∠SHO = 60˚
SO = 2√3
Найти:S полн. поверхности - ?
Решение:SH - апофема.
"Апофема - высота боковой грани правильной пирамиды, проведённая из вершины пирамиды".
△SHO - прямоугольный, так как SO - высота.
"Если угол прямоугольного треугольника равен 60°, то напротив лежащий катет равен произведению меньшего катера на √3".
=> SO = OH * √3 = 2√3 => OH = 2
"Сумма острых углов прямоугольного треугольника равна 90°".
=> ∠OSH = 90˚ - 60˚ = 30˚
"Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы".
=> SH = OH * 2 = 2 * 2 = 4
Так как данная пирамида - правильная, четырёхугольная => основание данной пирамиды - квадрат.
"Квадрат - геометрическая фигура, у которой все стороны равны".
=> АВ = ВС = AD = DC
AB = BC = AD = DC = 2 * OH = 2 * 2 = 4
S квадрата = 4² = 16 ед.кв.
Р - периметр квадрата.
Р = a * 4 = 4 * 4 = 16
S бок поверхности = 1/2Р * h = 16/2 * 2√3 = 16√3 ед.кв.
S осн = S квадрата.
S полн поверхности = S бок поверхности + S осн = 16√3 + 16 = 16(√3 + 1) ед.кв.
ответ: 16(√3 + 1) ед.кв.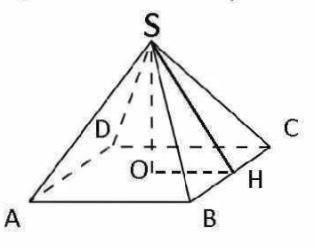
"Катеты прямоугольного треугольника равны 9см и 12см. В вершине прямого угла построен перпендикуляр к плоскости треугольника длиной 3см. Найти расстояния от концов перпендикуляра до гипотенузы. DA. это катет прямоугольного треугольника ADE. Второй катет известен, находишь гипотенузу DE."
Объяснение:
Расстоянием от А до СВ , будут АD, т.к АD⊥BС.
Расстоянием от Е до СВ , будут ЕD, т.к ЕD⊥BС по т. о трех перпендикуляра: если проекция АD перпендикулярна прямой лежащей в плоскости ВС, то и наклонная ЕD перпендикулярна ВС. .
1) ΔАВС-прямоугольный, по т. Пифагора СВ=√(9²+12²)=√225=15 (см).
По т. о среднем пропорциональном АС²=СD*СВ⇒ СD=144:15=9,6(см).
ΔАСD-прямоугольный , по т. Пифагора АD=√(12²-9,6²)=7,2 (см).
2)ΔАЕD-прямоугольный , по т. Пифагора ЕD=√(3²+7,2²)=7,8 (см).
1)В прямоугольном треугольнике ABC, угол А=90 градусов, АВ=20 см, высота АД=12 см.
Найти: АС и COS угла С.
ДВ"=АВ"-АД" = 400-144=256
ДВ=16
треугольники АВС и ДВА подобны по первому признаку подобия (два угла равны), следовательно ДВ/АВ=АВ/СВ
16/20=20/СВ
СВ=20*20:16=25
АС"=СВ"-АВ"=25"-20"=625-400=225
АС=15
мы нашли АС=15,
теперь ищем CosC
CosC=АС/СВ=15/25=3/5
CosC=3/5
ответ: CosC=3/5, АС=15см
2)
AD=AB cos A, S = AB AD sin A = AB² sin A cos A = 1/2 AB² sin(2A) = 72 sin(82°) = 72 cos(8°) ≈ 71,2993 см²