Тело вращения - цилиндр с радиусом основания, равным меньшей боковой стороне трапеции, с углублением в виде конуса того же радиуса.
Его площадь состоит из:
а) площади боковой поверхности конуса.
б) площади боковой поверхности цилиндра;
в) площади одного основания цилиндра.
Обозначим трапецию АВСD
а) S(бок.кон)=πrL
L– сторона CD трапеции. Высота трапеции СН "отсекает" от нее треугольник с катетами СН=АВ=8 и HD=AD-AH=16-10=6.
По т.Пифагора СD=10.
S(бок. конуса)=π•8•10=80π
б) S (бок. цил)=2π•r•h=2π•8•16=256π
в) S (осн)=πr²=π•8²=64π
S(полн)=π•(80+256+64)=400 π (ед. площади)
a) Модуль АМ=5.3 cм
б) (АВ-АС)*ВС= {0; 0; 0}
в) ∠ВДА=60°
г) векторы не колинеарны
Объяснение:
a) М(-0,5;1;2) СЕРЕДИНА ОТРЕЗКА ВС
АМ(-4,5;2;2)
Модуль АМ=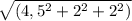
=5.3 cм
б) АВ-АС=(-6;1;2)-(-3;3;2)=(-3;-2;0)
(АВ-АС)*ВС=(-3;-2;0)*(3;2;0)= {0; 0; 0}
i j k
ax ay az
bx by bz
=
i j k
-3 -2 0
3 2 0
= i ((-2)·0 - 0·2) - j ((-3)·0 - 0·3) + k ((-3)·2 - (-2)·3) =
= i (0 - 0) - j (0 - 0) + k (-6 + 6) = {0; 0; 0}
в) Из ΔВДА найдем ∠ВДА по теореме косинуса, сторона лежащая напротив этого угла АВ
АВ^2=BD^2+AD^2-2BD*ADcos∠ВДА
Модуль АВ(-6;1;2)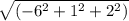 
=6,4 cм
Модуль ВС(3;2;0)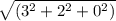 
=3,6 cм
Модуль АД(-1;2;7)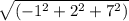 
=7,35 cм
6.4^2=3.6^2+7,35^2-2*3.6*7,35cos∠ВДА
cos∠ВДА=0,5; ∠ВДА=60°
г) Два вектора a и b коллинеарны, если существует число n такое, что
a = n · b
Векторы АВ(-6;1;2) АС(-3;3;2) АД (-1;2;7) имеют общее начало т А
Отношение координат разное (2; 1/3; 1) Поэтому векторы не колинеарны
первый рисунок слева
тк угол В 60° значит угол А 30°. сумма углов в треугольнике равна 180°
от сюда следует теорема, катет лежащий против угла в 30° равен половине гипотенузы, гипотенуза у нас ВА, 10:2=5 СМ
Да и если так, то ответы уже написаны. если нужно объяснить напиши в комментариях