Чтобы узнать, существует ли такой треугольник со сторонам 3; 3; 8 — надо сравнить каждую сторону с суммой друх других сторон: 8+3 = 11.
Каждая сумма двух сторон должна быть больше каждой стороны, чтобы такой треугольник существовал.
Сумма боковый сторон — 3+3 = 6, которая меньше стороны 8, тоесть треугольник со сторонами 3; 3; 8 — не существует.
Теперь представим, что боковые стороны равны 8; 8, а основание — 3.
3+8 = 11 > 3;
8+8 = 16 > 3
8+3 = 11 > 3.
В этом случае, треугольник сущестует, а основание — 3, боковые стороны — 8; 8.
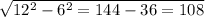
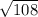
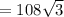
Эта задача на теорему косинусов, но для того, чтобы начать решать через теорему, нужно знать стороны. А для этого нам даны координаты. Найдем коориданты векторов AB,BC,AC. Для этого вспомним правило: чтобы найти координаты вектора, нужно из координат конца вектора, вычесть координаты начала вектора.
AB(1-0;-1-1; 2+1)=AB(1;-2;3)
BC(3-1;1+1;0-2)=BC(2;2;-2)
AC(3-0;1-1;0+1)=AC(3;0;1)
Теперь найдем длину этих векторов.
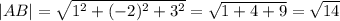
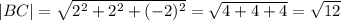
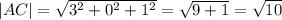
Теперь запишем теорему косинусов, используя косинус угла С.
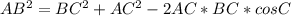
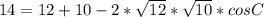
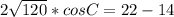
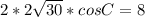
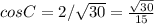
Нужно все проверить!
2 стороны при прибавлении должны быть больше третьей стороны. Поэтому берём 8 боковые стороны,а основание 3