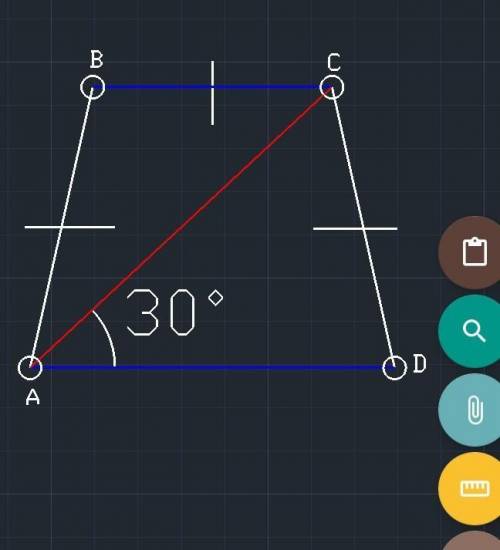
1)Поскольку ВС и AD - параллельны по свойству трапеции, (основания параллельны) то АС - секущая,
( красным - секущая; синим - основания)
Тогда по теореме накрест лежащих углов получаем следующее равенство:
{< - угол} <САD=<ACB=30°, поскольку накрест лежащие углы равны
2) Из пункта 1 и условия следует, что если рассмотреть
{∆ - треугольник} ∆АВС, то он равнобедренный, а значит <АСВ=<САВ=30°
Так как <А=<ВАС+<САD, то, он равен 60°
3) Поскольку из свойств равнобедренной трапеции следует, что углы при основании равны, поэтому
<D=60° как и <В=<С
4),Сумма односторонних углов равна 180° при секущей СD, и параллельных прямых ВС и AD из чего так же следует, что
<В=180°-60°=120°, => <С=120°
ответ: 120°, 120°, 60°, 60°
См. рисунок и объяснения.
Объяснение:
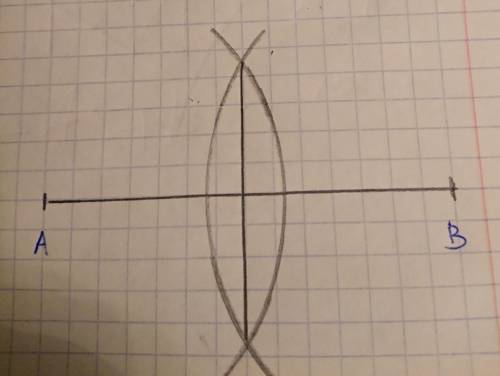
В данном случае предпологается, что линейка без делений. Т.е. просто инструмент для проведения линий.
Берём циркуль и выставляем ножки циркуля на расстояние чуть боьше середины отрезка (примерно 1-2 см). Проводим окружность с центром в одном конце отрезка и другую окружность с центром в другом конце отрезка.
Поскольку окружности одинаковые, то пересечения будут симметричные.
Дальше линейкой соединяем точки пересечения окружностей. Полученный отрезок будет перпендикуляерн первоначальному и бедут делить его пополам.
складываем части 2+3+5=10 делим 180/10=18
<А=18*2=36 <В=18*3=54 <С=18*5=90
то треугольник прямоугольный, самая длинная АБ ибо гипотенуза