
3.
<ADC — прямой, тоесть треугольник ADC - прямоугольный.
Гипотенуза AC = 7; катет DC = 3.5, можно также заметить, что этот же катет равен половине гипотенузы.
Теорема о 30-градусном угле прямоугольного треугольника такова: сторона, противолежащая углу 30-и градусов в прямоугольном треугольнике — равен половине гипотенузы, что и означает, что <DAC, который лежит против DC — равен 30°.
<DAC = 30° ⇒ <D = 90-30 = 60°.
AC == AB ⇒ <B == <C = 60°
<A = 180-(60+60) = 60°
<DAC = 90° ⇒ <D = 90+90 = 180° (сумма смежных углов равна 180°).
Вывод: <B = 60°; <D = 180°.
4.
AC == AD ⇒ CF — и высота, и медиана, и биссектриса.
<ACD == <FCD = 30°
По теореме 30-градусного угла прямоугольного треугольника — BF (противолежит углу 30-и градусов) = CF/2 ⇒ BF = 2.
Вывод: BF = 2.
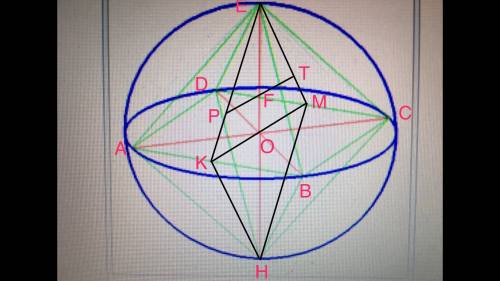
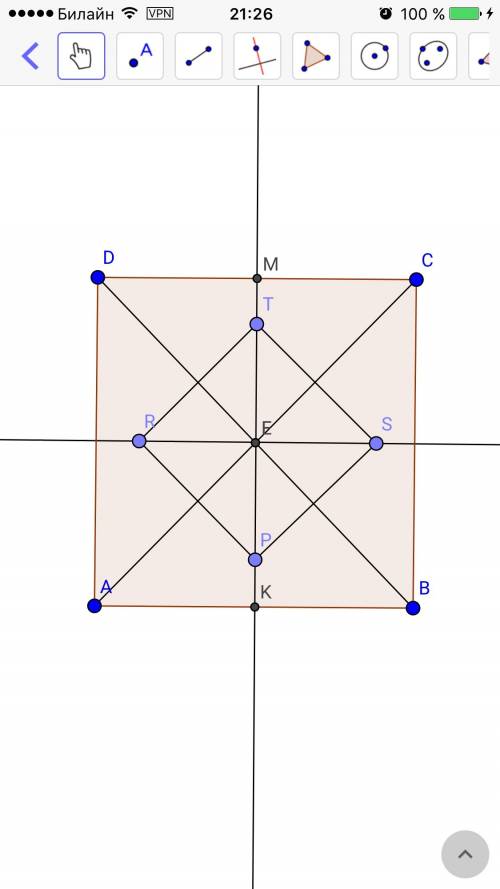
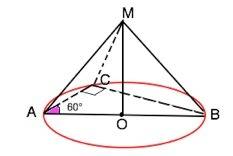
Обозначим пирамиду МАВС, МО - высота, угол С=90°, угол САВ=60°, ВС=4√3.
а) Вокруг основания треугольной пирамиды можно описать окружность. Так как все ребра пирамиды наклонены к плоскости основания под равным углом, их проекции равны радиусу описанной окружности, и основание высоты пирамиды - центр описанной окружности.
Центр окружности, описанной вокруг прямоугольного треугольника - середина гипотенузы, ч.т.д.
б) Боковые ребра данной пирамиды - наклонные с равными проекциями, следовательно они равны гипотенузам равнобедренных треугольников с катетами МО - высота пирамиды, и ВО=АО=СО - радиус описанной окружности основания.
АВ=АС:sin60°
АВ=4√3:(√3/2)=8
OB=8:2=4
MB=MA=MC=OB:sin45°=4:√2/2=4√2 (ед. длины)
В 4) вф равно 2