
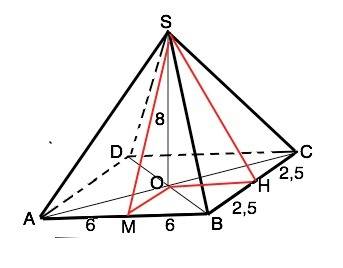
Основание пирамиды прямоугольник.
Его площадь 12•5=60 см²
Диагонали прямоугольника равны и в точке пересечения делятся пополам ⇒АО=ОВ=ОС=OD. Эти половинки диагоналей - проекции ребер пирамиды. Следовательно, ребра пирамиды как наклонные с равными проекциями равны. SA=SD=SC=SB
Боковые грани – 2 пары равных равнобедренных треугольников с основаниями 12 см и 15 см.
Высота SМ в ∆ASB=√(SO*+OM*)=√(64+6,25)=0,5√281
Высота SН в ∆BSC=√(SO²+OH²)=√(64+36)=10 см
S ∆ASB=AM•SM=6•0,5√281=3√281 см²
S ∆ BSC=BH•SH=2,5•10=25 см²
S бок=2•3√281+2•25=(6√281+50) см² или ≈150,58 см²
S полн=60+60√281+50=(110+60√281) см² или ≈210,58 см²
б) проведем высоту cl , из прямоугольного треугольника cld
ld²=cd²-ab²=25²-24²=49
ld=7
если в четырехугольник вписана окружность,то сумма его противоположных сторон равна .
ab+cd=bc+ad
bc+ad=49
ad=bc+ld
bc+bc+ld=49
2bc+7=49
bc=21
ad=49-21=28
в)проведем радиус qf ,точка f лежит на прямой cd
qf является высотой т. к. касательная к окружности перпендикулярна радиусу.
отметим на прямых bc и ad точки к и м ,так что бы км являлось диаметром и была параллельна ab,далее из свойств прямоугольной трапеции ,В которую вписана окружность
kc=cf=bc-r=21-12=9
ed=ef=ad-r=28-12=16
qf является высотой треугольника cdq, в прямоугольном треугольнике квадрат высоты равен произведению отрезков ,на которые высота делит гипотенузу
qf²=16*9
12²=16*9
144=144
следовательно треугольник cdq прямоугольный