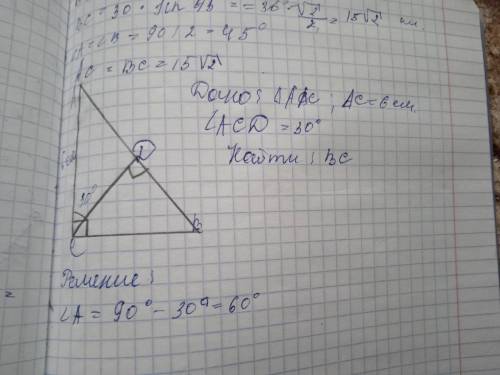
Углы, образованные при пересечении двух параллельных прямых секущей, или равны, или в сумме составляют 180°. Следовательно, нам дано значение одного из смежных углов.
а) второй угол равен 180° - 150° =30°.
б) один из углов равен Х градусов, второй - Х+70 градусов. Их сумма равна 2Х+70=180° => X=55°. Тогда меньший угол = 55°, второй = 125°.
Или (см. рисунок): а) <1=<4=<5=<8 =150°, <2=<3=<6=<7=30°.
б) <1=<4=<5=<8 =125°, <2=<3=<6=<7=55°.
P.S.
<1=<4, <5=<8, <2=<3 и <6=<7 как вертикальные,
<4=<5 и <3=<6 как внутренние накрест лежащие.
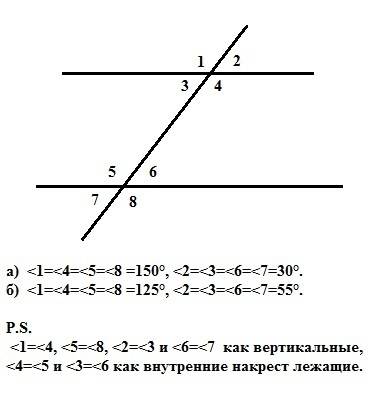
<ACD = 30° => AD = CA/2 (теорема 30-градусного угла прямоугольного треугольника).
AD = 6/2 = 3 =>
По теореме Пифагора, зная один катет и гипотенузу:![CD = \sqrt{AC^2-AD^2}\\CD = \sqrt{6^2+3^2} \Rightarrow CD = \sqrt{45]\\CD = 6.7.](/tpl/images/1744/5211/73bd1.png)
<ACD = 30° => <DCB = 90-30 = 60° => <B = 90-60 = 30°.
По теореме 30-градусного угла прямоугольного треугольника: катет, противолежащй углу 30-и градусов в прямоугольном треугольнике — равен половине гипотенузы, тоесть: CD = CB/2 => CB = CD*2 = 6.7*2.
Вывод: CD = 13.4.