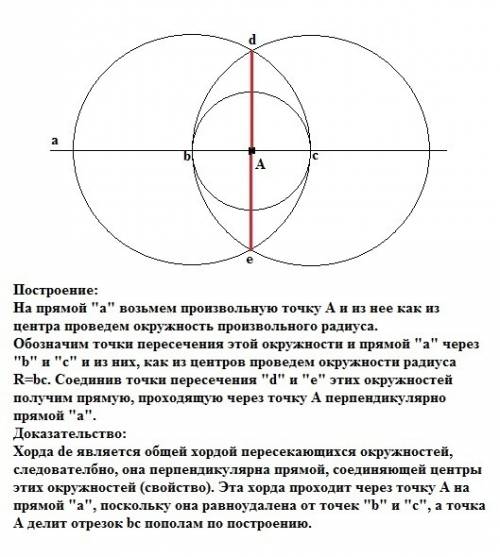
Построение:
На прямой "а" возьмем произвольную точку А и из нее как из центра проведем окружность произвольного радиуса. Обозначим точку пересечения этой окружности с прямой "а" через "b" и "с" и из них, как из центров проведем окружности радиуса R=bс. Соединив точку пересечения "d" и "е" этих окружностей получим прямую, проходящую через точку А перпендикулярно прямой "а".
Доказательство:
Хорда de является общей хордой пересекающихся окружностей, следовательно, она перпендикулярна прямой, соединяющей центры этих окружностей (свойство). Эта хорда проходит через точку А на прямой "а", поскольку она равноудалена от точек "b" и "с", а точка А делит отрезок bс пополам по построению.
∢К=∢М=180-60=120°
MK=12*2=24
S ромба=0,5*d1*d2
Обозначим вторую диагональ(NL) через х:
288√3=0,5*24*x
Х=24√3(NL)
По теореме Пифагора найдём сторону ромба:
(12√3)²+12²=432+144=576
√576=24
Мы знаем что все стороны ромба одинаковые, найдём периметр:
Р=24+24+24+24=96мм
р=96÷2=48мм
∢ МКN=120÷2=60
Значит другой угол равен:
180-(60+90)=30°(∢О)
По теореме сторона лежащий против 30° равен половине гипотенузы:
Гипотенуза ОК=12
12÷2=6(катет)
По теореме Пифагора найдём другой катет(r)
144-36=108
r=√108=6√3
Площадь круга:
S=пr²=108п
ответ:р=48мм
r=6√3 мм
S=108п