
Пусть B-Начало координат
Ось X - BC
Ось Y - перпендикулярно X в сторону A
Ось Z - MB
Найдем MB из треугольника MAB = √(6^2-3^2)= 3√3
Координаты точек
E (1/2;√3/2;0)
D (2,5;√3/2;0)
L( 1;√3;√3)
Уравнение плоскости основания ABC
z=0
Уравнение плоскости EDL
ax+by+cz+d=0
Подставляем координаты точек E D L
a/2+√3b/2+d=0
2,5a+√3b/2 + d =0
a+√3b+√3c + d=0
a=0 Пусть d = - √3/2 тогда b=1 c= -1/2
Уравнение EDL
y - z/2 -√3/2=0
Косинус искомого угла равен
| (0;0;1) * (0;1;-1/2) | / | (0;0;1) | / | (0;1;-1/2) | = 1/√5
Cам угол - arccos(√5/5)
ответ: ≈11.66.
Объяснение:
Решение.
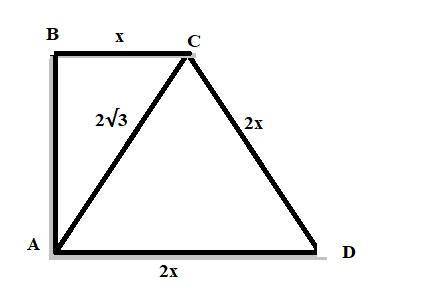
По условию треугольник ACD - равнобедренный:
Если ВС=х, то AD=CD=2x/
Угол при вершине (угол D) равен 60°.
∠CAD=∠ACD=60°/ Следовательно ΔACD-равносторонний со сторонами равными 2√3.
По условию AD=2x; ВС=х. Тогда
ВС=1/2AD;
ВС=1/2*2√3;
ВС=√3.
------------------
По построению получается, что трапеция Прямоугольная (См. скриншот).
Находим сторону АВ:
Из прямоугольного треугольника АВС по т. Пифагора
АВ²=АС²-ВС²=(2√3)²-(√3)²=12-3=9;
АВ=√9=3. Тогда периметр трапеции
P=AB+BC+CD+AD=3+√3+2√3+2√3=3+5√3≈11.66.
Объяснение:
Медианы треугольника пересекаются и в точке пересечения делятся в отношении 2:1, считая от вершины.
ВО : ОN = 2 : 1
ВО = 6
следовательно
ОN = 3