Поверхность параллепипеда состоит из 2х оснований и боковой поверхности.
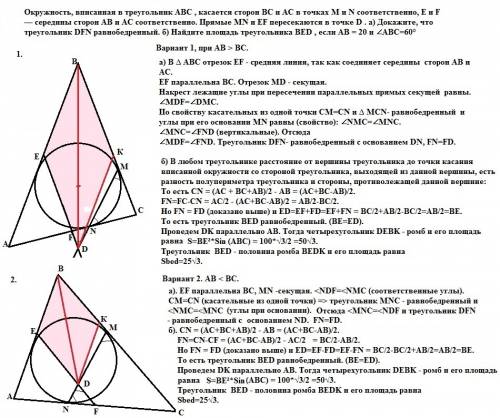
Площадь основания Sосн = а*в*sin60 = 15*8*√3/2 = 60√3 cм²
Боковая поверхность Sбок = 2(а+в)*h = 46h
Диагональное сечение представляет собой прямоугольник с высотой h и шириной равной диагонали основания. s=130 cм²
Диагональ найдем, как третью сторону треугольника с=√(а² + b² - 2аb·cos60) =
= √64+225-2*8*15*0,5 = √169 = 13 cм
Высоту найдем h = s/c = 130/13 = 10 cм
S = 2*60√3 + 46h = 120√3 + 460 cм²
Основанием параллелепипеда является параллелограмм со сторонами
а = 8см и в = 15см, угол между ними α = 60°.
Найдём меньшую диагональ d параллелограмма по теореме косинусов:
d² = а² + в² - 2ав·cosα
d² = 8² + 15² - 2·8·15·0.5 = 64 +225 - 120 = 169
d = 13(cм)
Меньшее диагональное сечение параллелепипеда является прямоугольником со сторонами d и Н (высота параллелепипеда).
S cеч = d · Н
По условия S cеч = 130см²
d · Н = 130
13·Н = 130
Н = 10(см)
Площадь основания параллелепипеда:
Sосн = а·в·sin 60° = 8·15·0.5√3 = 60√3(cм²)
Периметр параллелограмма
Р = 2(а + в) = 2·(8 + 15) = 46(см)
Площадь боковой поверхности
S бок = Р·Н = 46· 10 = 460(см²)
Площадь полной поверхности параллелепипеда:
S = 2Sосн + Sбок = 2·60√3 + 460 = 120√3 + 460 ≈ 668(см²)
ответ: S = 120√3 + 460 ≈ 668(см²)