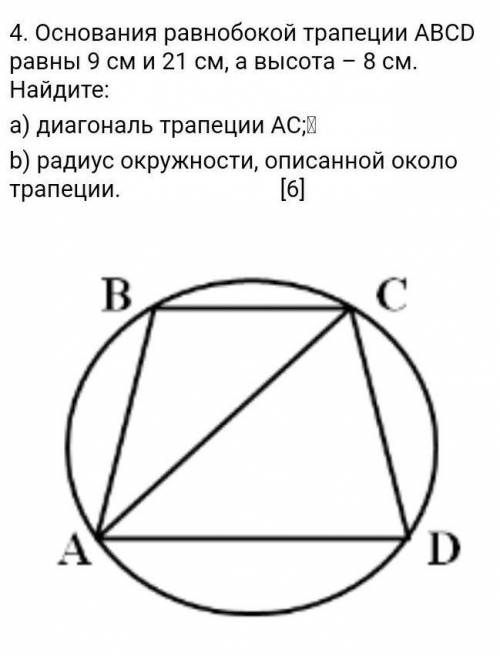
т.к AB не параллельна плоскости, значит будем считать, что плоскость провели через сторону AD и А является тупым углом ромба. Сторону ромба обозначим Ы.
из точки А на сторону BC опустим высоту AH. Поскольку острый угол ромба равен 45, AH = BH = Ы / sqrt(2)
ВС || a т.к BC || AD и AD принадлежит а.
Проекции точек B и H на плоскость а обозначим В' и H' соответственно.
т.к ВС || a, то BH || B'H' и вообще BHH'B является параллелограмом.
из прямоугольного треугольника АВВ' , где ВАВ' = 30 получаем B'A = Ы sqrt(3)/2
в прямоугольном треугольнике AB'H' AH' = sqrt(AB' ^2 - B'H' ^2) = sqrt(3/4 - 1/2)Ы = Ы/2
плоскость треугольника AHH' перпендикулярна плоскости ромба и плоскости а, поэтому угол HAH' является углом между искомыми плоскостями
и равен arccos(AH' / AH) = arccos(Ы/2 : Ы/sqrt(2)) = arccos(1/sqrt(2)) = 45
на ютубе вбей вопрос, решение там есть