∠B = 30°
Пояснение:
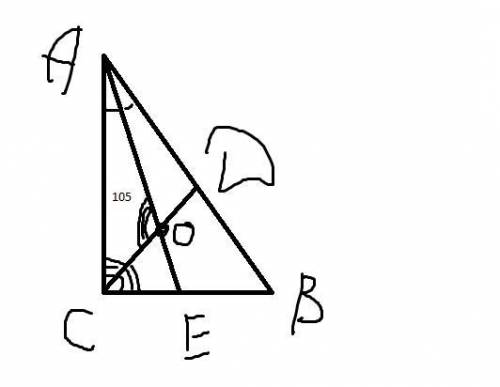
Дано: Δ АВС, ∠С = 90°, ∠АОС = 105°, биссектрисы CD и АЕ, что пересекаются в точке О
Найти: меньший острый угол Δ АВС
Решение
∠CAO = ∠OAD (так как биссетриса AE делит угол ∠А пополам)
∠ACD = ∠OCB= ∠C/2 = 90°/2 = 45° (так как биссетриса CD делит угол ∠C пополам)
Рассмотрим Δ CAO, в котором ∠CAO = 45°, ∠АОС = 105°, ∠CAO - ?
Так как сумма всех углов в треугольнике равна 180°, то
∠CAO = 180° - (105° + 45°) = 180° - 150° = 30°
∠CAO = ∠OAD = 30°, следовательно ∠А = ∠CAO + ∠OAD = 60°
Рассмотрим Δ АВС, в котором ∠С = 90°, ∠А= 60, ∠B - ?
Так как сумма углов при катетах в прямоугольном треугольнике равна 90°, то
∠B = 90° - ∠А = 90° - 60° = 30°
ответ: ∠B = 30°
30°
Объяснение:
В равнобедренном треугольнике два угла одинаковые (у основания), а третий отличается. Сумма углов треугольника = 180°.
Т.о. может быть два варианта:
1. Углы у основания больше в 2,5 раза третьего угла
2. Углы у основания меньше в 2,5 раза третьего угла
Пусть углы у основания будут = a = b
Третий угол c
Вариант 1:
a = b = 2.5 c
a + b + c = 180°
2,5c + 2,5c + c = 180°
6c = 180°
c = 180°/3 = 30°
Наименьший угол с = 30°
Вариант 2:
a = b = c/2.5 = c*(2/5)
a + b + c = 180°
c * (2/5) + c* (2/5) + c = 180°
c ( 1 + 4/5) = 180°
c = 5* 180°/9 = 100°
a = b = c*2/5 = 40°
В первом вартанте наимельший уголо меньше. Значит ответ задачи 30°
ой кажись не то отправила