Боковая поверхность пирамиды равна сумме площадей 3х граней (треугольников)
Высота основания h=a√3/2, площадь основания S = a*h/2 = a²√3/4, отсюда
а = √4S/√3 = √4*36√3/√3 = 12
Высота пирамиды H = h*tg 30 = 6√3*1/√3 = 6, апофема А=√h²+Н²=√36*3+36=12
S = a*H/2+a*H/2+a*A/2 = 12*6+12*12/2 = 72+72 = 144
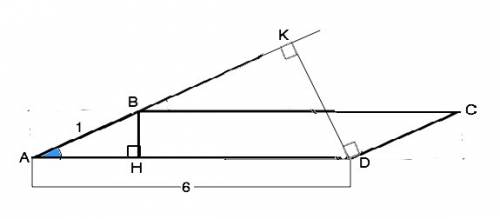
Одна из формул площади параллелограмма Ѕ=a•h. Очевидно, что при одинаковой площади большей будет высота, проведенная к меньшей стороне, и наоборот. Следовательно, искомой будет высота к стороне АВ ( или равной ей CD).
На рисунке в приложении высота к меньшей стороне АВ пересекается с ее продолжением. Из прямоугольного треугольника AKD высота DK=AD•sinA=6•1/3=2 (ед. длины)
Как вариант можно найти большую высоту иначе. Сначала найти длину меньшей высоты ВН=АВ•sinA, затем найти площадь S=ВН•AD и высоту DK=S:AB.
Использованы: формула площади правильного треугольника, формула высоты правильного треугольника, определение тангенса, косинуса, формула площади треугольника