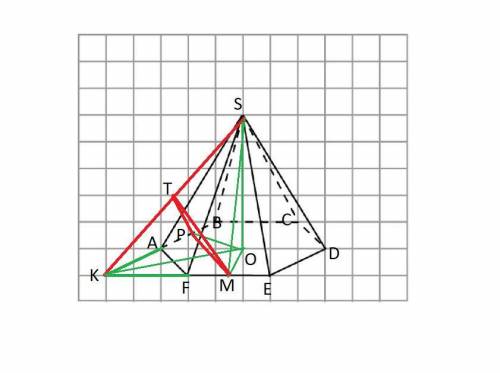
Отрезок KS - линия пересечения заданных плоскостей.
Проекция апофемы на основание равна радиусу вписанной окружности.
r = OM = 2*cos30° = 2*(√3/2) = √3.
Высота пирамиды Н = √(17 - 2²) = √13.
Отрезок КО равен 2√3.
Длина KS = √(13 + (2√3)²) = √25 = 5.
Из точек М и Р проводим перпендикуляры к KS.
Длина МР как средняя линия трапеции ABEF равна (2 + 4)/2 = 3.
Апофема SM равна √(13 + (√3)²) = √16 = 4.
Отрезки РТ и МТ = 3*sin(MKS) = 3*(4/5) = 12/5.
Искомый угол равен:
α = 2arc sin((3/2)/(12/5) = 2arc sin(5/8) = 77,36437°.
ВВ₁ и DD₁ - медианы, значит
AD₁ = D₁B = AB₁ = B₁D = 3/2 см
ΔABD равнобедренный, поэтому
∠ABD = ∠ADB,
BD₁ = DB₁, BD - общая сторона для ΔDD₁B и ΔBB₁D, значит эти треугольники равны по двум сторонам и углу между ними, ⇒
BB₁ = DD₁.
Медианы точкой пересечения делятся в отношении 2 : 1, считая от вершины.
Обозначим OD₁ = OB₁ = x, тогда OD = OB = 2x.
ΔOBD равнобедренный, значит ∠OBD = ∠ODB = 40°.
∠D₁OB = ∠OBD + ∠ODB = 80° как внешний угол ΔDOB.
Рассмотрим ΔD₁OB. По теореме косинусов
D₁B² = OD₁² + OB² - 2·OD₁·OB·cos 80°
9/4 = x² + 4x² - 2 · x · 2x · cos80°
9/4 = 5x² - 4x² · cos80°
9/4 = x² (5 - 4cos80°)
x² = 9 / (4(5 - 4cos80°))
x = 3 / (2√(5 - 4cos80°))
BB₁ = 3x = 9 / (2√(5 - 4cos80°)) или
Если необходимо числовое значение, а не выражение, можно взять значение cos 80° по таблице, тогда получится:
cos 80° ≈ 0,1736
BB₁ = 9 / (2√(5 - 4cos80°)) ≈ 2,2