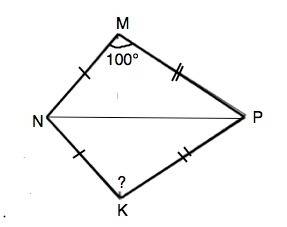
1)
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
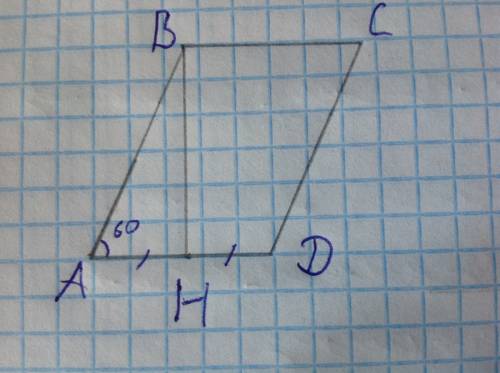
2)
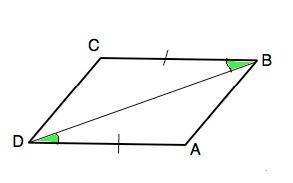
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
Из равенства треугольников АКО и АРО следует АК=АР=8 см, Из равенства треугольников BNO и BPO следует BN=BP=12 см.
CKON - квадрат, CK=CN=r, АС=8+r, CB=12+r
По т. Пифагора
Получаем
Т к
AC=12 см, CB=16 см, S=