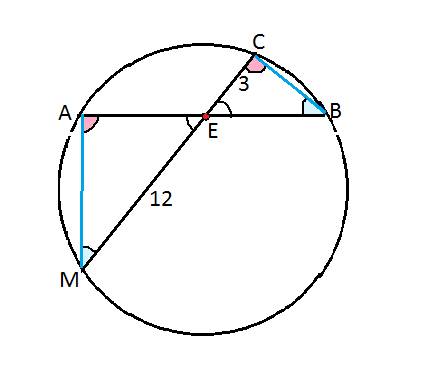
Рассмотрим ∆ АВD и ∆ СВЕ
Оба прямоугольные и имеют общий острые угол АВС.
Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
Из подобия следует отношение
ВЕ:ВD=ВС:АВ⇒ВD•ВС=ВЕ•АВ ⇒
ВЕ:ВС=ВD:АВ
Две стороны ∆ ВЕD пропорциональны двум сторонам треугольника АВС, и угол между ними общий.
2-й признак подобия треугольников:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Следовательно, ∆АВС и ∆ ВЕD подобны, что и требовалось доказать.
Можно добавить. что коэффициент подобия равен косинусу общего угла, т.к. отношение катетов ∆ СВЕ и ∆ АВД к их гипотенузам соответственно равны косинусу угла В треугольника АВС.

так как треуольник равнобедеренный, значит у него две стороны равны, если один угол тупоугольный, значит он лежит против основания, так как в треугольнике не может быть два угла больше 90°, а также основание большая сторона, так как лежит против наибольшего угла, значит основание x, а две боковые равны по x-3
x+x-3+x-3=24
3x=30
x=10
Основание = 10;
Боковые = 7