(Сделай лучшим)
(Рисунок к задаче 8)
6) Дано:
Трикутник ABC
Кут BAZ = 150° (точка z - за межею завершенного відрізка CA)
Кут ACB = 110°
x - ?
Розв'язання:
Кут CAB, за властивістю суміжних кутів (сума суміжних кутів дорівнює 180°) дорівнює 180°-150°=30°. Сума всіх кутів трикутника дорівнює 180°. 180-110-30=40° (кут ABC). Знову використовуємо властивість суміжних кутів. 180-40=140° = x
Відповідь: x = 140°
7) Дано:
Трикутник ABC
Вертикальний кут до кута CAB = 62°
Кут ABC = 80°
x - ?
Розв'язання:
Кут, що даний і дорівнює 62° вертикальний до кута CAB, а оскільки вертикальні кути дорівнюють один одному - кут CAB дорівнює 62°. Сума всіх кутів трикутника дорівнює 180°. Кут BCA дорівнює 180°-80°-62°=38°. Оскільки вертикальні кути дорівнюють один одному то кут вертикальний до кута BCA дорівнює йому. Їх сума - 76°. Коло - 360°. x = (360-76)/2=142°
Відповідь: x = 142°
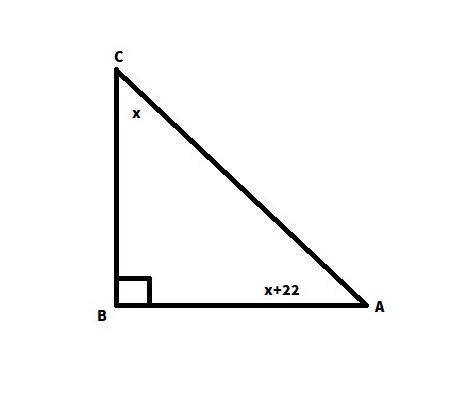
8) Дано:
Трикутник ABC (Кут B = 90°)
Кут A - Кут C = 22°
Кут C - ?
Розв'язання:
Сума всіх кутів трикутника дорівнює 180°. Сума двох гострих кутів прямокутного трикутника дорівнює 90°.
90° = x + x +22°.
68°=2x
34°=x=Кут С
Відповідь: Кут С (менший з гострих кутів трикутника) дорівнює 34°
(см. объяснение)
Объяснение:
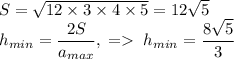
Сразу замечу, что задача составлена неграмотно. Высота измеряется в сантиметрах, а не сантиметрах квадратных, поэтому правильного ответа здесь заведомо нет! Если пренебречь этой существенной неточностью, видим, что в последнем варианте не сокращена дробь, хотя 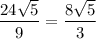 .
.
Комментарий:
Задачу можно было решить, не зная формулы Герона (хотя она есть в школьной программе).
Покажем, что достаточно уметь применять теорему Пифагора:
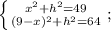
Решая систему, получаем, что 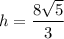 .
.
Однако такой подход, как мне кажется, менее оптимален.
Задание выполнено!
кароч я незнаю но напишу просто пвлвововтвлвлвтвт волвтвлвлч 1000+₽7₽+3(38₽+₽;₽+
Объяснение:
рвожражоаожагжаос мпрлишп Часмаго арлрсроирв