Диагонали параллелограмма равны 14 и 
Объяснение:
Маленькое замечание. Понятно, что диагональ, на которую опущен перпендикуляр, равна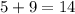 
. Но число, фигурирующее в ответе и получающееся при решении задачи, 
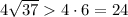— бОльшая диагональ, значит именно она лежит против тупого угла параллелограмма. Получается, что в условии фраза «перпендикуляр, проведенный из вершины тупого угла» ложна.
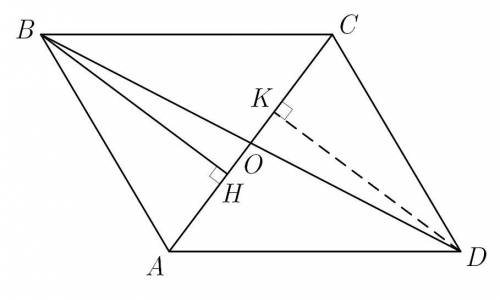
Пусть высота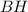 
, проведенная к диагонали 
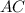, делит ее на отрезки 
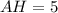и 
.
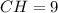Так как периметр параллелограмма состоит из двух пар равных сторон, то сумма двух смежных сторон параллелограмма равна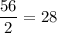 
. Пусть 
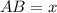, тогда 
.
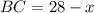По теореме Пифагора из треугольника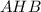 
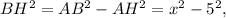
а из треугольника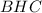 
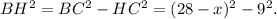
Приравнивая полученные выражения, получаем
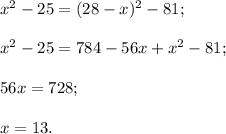
Тогда
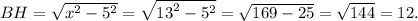
Если из вершины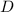 
опустить перпендикуляр на диагональ 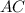, то треугольник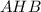и и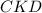 
будут равны, 
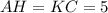, значит 
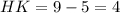, а
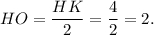
Из треугольника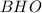 
по теореме Пифагора
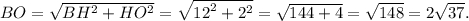
Тогда вторая диагональ параллелограмма
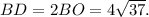
Відповідь:
Пояснення:
1 . BC = √(AB² - AC²) = √( 87² - 60² ) = √3969 = 63 ( см ) . Тоді
сtgA = AC/BC = 60/63 = 20/21 .
В - дь : сtgA = 20/21 .
2 . Проведемо ВМ⊥АС . АС = 3 + 14 = 17 ( см ) .
S ΔABC = 1/2 AC * BM ; BM = 2 * S ΔABC/AC = 2 * 170/17 = 20 ( cм ) .
S ΔABD = 1/2 AD * BM = 1/2 * 3 * 20 = 30 ( см² ) .
В - дь : 30 см² .