Пусть дан треугольник АВС, у которого АВ=2см, ВС=4см, АС=3см. Проведем биссектрисы AF, BK, CE, которые пересекаются в точке О. По свойству биссетрисы треугольника : биссектриса делит противолежащую сторону треугольника на отрезки пропорциональные двум другим сторонам.
Рассмотрим биссетрису ВК, применяя описанное свойство, имеем:
АК:КС=АВ:ВС
АК:КС=2:4=1:2
Значит сторона АС состоит из 1+2=3 равных части. А так как АС=3 см, то одна часть составляет 1см, то АК=1 см, КС=2см.
Рассмотрим треугольник ВСК, в нем СО - биссетриса.Используя тоже свойство, получим:
ВО:КО=ВС:СК
ВО:КО=4:2=2:1
Значит точка О делит биссектрису, проведенную из точки В в отношении 2:1
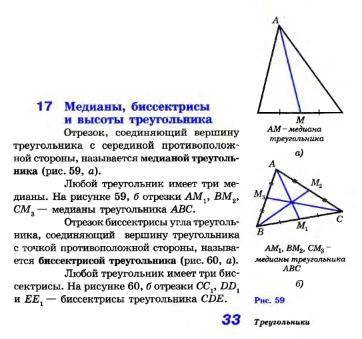
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)
Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)
Любой треугольник имеет:
· три медианы (рис. 59 б)
· три биссектрисы (рис. 60 б)
· три высоты (рис. 62 а, б, в)
Свойства:
- в любом треугольнике медианы пересекаются в одной точке.
- в любом треугольнике биссектрисы пересекаются в одной точке.
- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

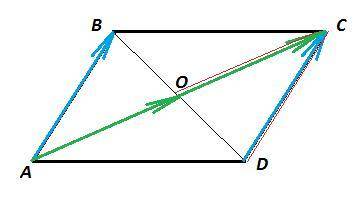
В параллелограмме противоположные стороны попарно параллельны и равны. Диагонали параллелограмма точкой пересечения делятся пополам.
=======================================
1. AB = x*СD; x = 1 - если вопрос касается длин отрезков
x = -1 - если вопрос касается векторов
2. AC = x*AO; x = 2
3. OB = x*BD; x = 0,5 - если вопрос касается длин отрезков
x = -0,5 - если вопрос касается векторов
4. OC = x*CD; определить значение х невозможно, так как длина одной диагонали и длина одной стороны параллелограмма в общем случае никак не связаны.
Нисколько не посягая на приоритет Лоры, я вот что сделаю -
обозначу a = CB = 4; b = AC = 3; c = AB = 2; (Угол В лежит напротив стороны b.)
Точка О - точка пересечения биссектрис. ВМ - биссектриса угла В, М лежит на АС.
Сторона b делится на отрезки, отношение которых
АМ/МС= c/a, а их сумма АМ + МС = b.
Легко увидеть, что эти отрезки имеют длины СМ = b*a/(a+c) и АМ = b*c/(a+c);
Биссектриса угла В делится биссектрисой угла А в отношении BO/OM = AB/AM; считая от вершины В.
ВО/ОМ = c/(b*c/(a+c)) = (a+c)/b;
это очень полезная формула. В условиях задачи ВО/ОМ = (4 + 2)/3 = 2;