Нарисуем параллелограмм и обозначим его вершины как АВСД.
Проведем высоты ВН из В к АД, и ВО из В к СД.
Высоты образовали со сторонами параллелограмма два треугольника. Они прямоугольные и подобны, т.к. острые углы при А и С в них равны.
Все элементы подобных треугольников имеют равный коэффициент подобия. Следовательно, гипотенузы АВ и ВС образовавшихся треугольников АВН и ВСО относятся как 2:3
Обозначим коэффициент этого отношения х.
Тогда АВ:ВС=2х:3х
АВ+ВС=5х
АВ+ВС=60:2=30 cм
5х=30 cм
х=6 см
АВ=2*6=12 см
ВС=3*6=18 см
Большая сторона параллелограмма равна 18 см
Записать решение кратко труда не составит.
Пусть меньшая сторона параллелогамма равна а, высота, проведенная к этой стороне равна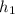
, а острый угол между сторонами параллелограмма равен 
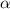. Большая сторона параллелограмма пусть равна b, высота, проведенная к этой стороне равна 
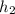. По условию задачи 
.
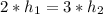То есть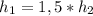
. Если вычислить площадь параллелограмма, то по одной из формул будет
Приравняем два полученных выражения площади
Получается, что
Так как по условию задачи периметр параллелограмма равен 60 см, то
Используя что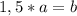
, получаем
а=12. Тогда b=1,5*a, b=18 см.
Значит большая сторона параллелограмма равна 18 см.