Объяснение:
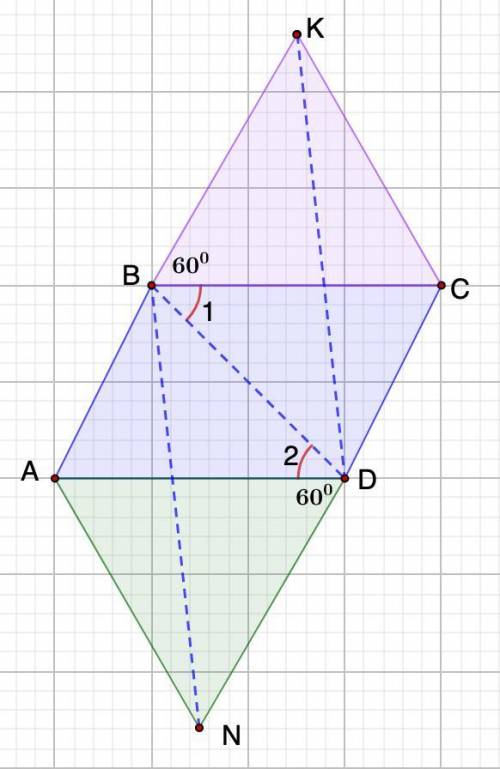
Дано: ABCD - параллелограмм.
ΔВКС и ΔAND - равносторонние.
Доказать: BKDN - параллелограмм.
Доказательство:
1. Рассмотрим ΔВКС и ΔAND - равносторонние.
Противоположные стороны параллелограмма равны.⇒ ВС = AD
⇒ ΔВКС = ΔAND (по трем сторонам, 3 признак)
⇒ BK = ND
2. ВС || AD (ABCD - параллелограмм)
∠1 = ∠2 (накрест лежащие при ВС || AD и секущей BD)
В равностороннем треугольнике углы равны 60°.⇒
∠DBK = ∠1 + 60°
∠BDN = ∠2 + 60°
⇒ ∠DBK + ∠BDN - накрест лежащие при BK и ND и секущей BD.
Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.⇒ BK || ND
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.⇒ BKDN — параллелограмм
ответ: стороны треугольника 13; 14; 15
Объяснение: проведенные отрезки - это биссектрисы данного треугольника (центр вписанной окружности - точка пересечения биссектрис треугольника);
получившиеся треугольники имеют равные высоты - это радиус вписанной окружности (любая точка биссектрисы угла равноудалена от сторон угла; радиус, проведенный в точку касания перпендикулярен касательной)
площади треугольников, имеющих равные высоты относятся как основания; получим отношения сторон треугольника (для определенности обозначим сторону (а) у треугольника с площадью 30; сторона (b) у треугольника площадью 28; (с) для площади 26):
а/b = 30/28 = 15/14
a/c = 30/26 = 15/13
b/c = 28/26 = 14/13
можно записать три стороны:
a = 15c/13; b = 14c/13 и с.
площадь всего треугольника = 30+28+26 = 84 и она связана со сторонами по формуле Герона)
полупериметр = ((15/13)+(14/13)+1)*(c/2) = 21c/13
84 = корень из((21с/13)*(6c/13)*(7c/13)*(8c/13))
84 = 7*3*4*c^2/169
c^2 = 169
c = 13
b = 14
a = 15