Объяснение:
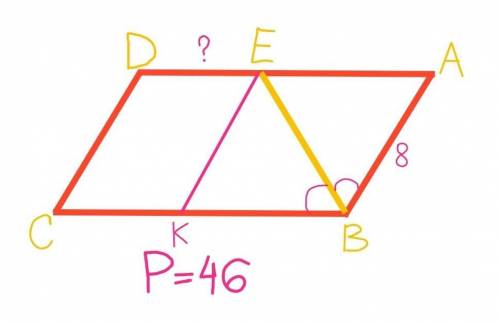
Из точки Е проведем отрезок ЕК, параллельный АВ.
Противоположные стороны параллелограмма параллельны, тоесть СВ//DE => ЕА//КВ и DE//CK
Так как в четырехугольнике КЕАВ стороны попарно параллельны, следовательно КЕАВ – параллелограмм.
ВЕ – биссектриса угла КВА по условию и диагональ параллелограмма КЕАВ.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб.
Следовательно: КЕАВ – ромб
У ромба все стороны равны. Исходя из этого: ЕА=КВ=АВ=8 см.
СD=AB=8 так как противоположные стороны параллелограмма равны.
Р(АВСD)=АВ+ВС+CD+AD=AB+BK+KC+CD+DE+EA=8+8+KC+8+DE+8=32+KC+DE
Так как Р(ABCD)=46 см по условию, то получим уравнение:
32+КС+DE=46
KC+DE=14 см
Так как ЕК//АВ, а АВ//CD, то ЕК//CD;
DE//CK (доказано ранее);
Исходя из этого: CDEK – параллелограмм.
Противоположные стороны параллелограмма равны, тоесть DE=CK.
Тогда 2DE=14 см
DE=7 см
ответ: 7 см
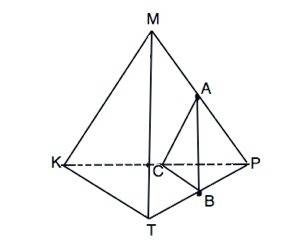
По условию секущая плоскость параллельна плоскости КМТ.
Точки А и В лежат в плоскости грани МРТ и являются серединами сторон МР и ТР треугольника МТР.
Следваоетльно, прямая АВ параллельна МТ.
Из т.В проведем прямую ВС параллельно КТ.
ВС - средняя линия ∆ КТР.
С- середина КР, АС - средняя линия ∆ МКР и параллельна МК.
Две пересекающиеся прямые АВ и МС плоскости АВС параллельны двум пересекающимся прямым МТ и ТК плоскости МКТ. Это признак параллельности плоскостей, следовательно, АВС - искомое сечение.
Трапеция АВСD, Углы А и В прямые, CD - наклонная (большая) боковая сторона, точка касания вписанной окружности делит CD на отрезки 4 и 25 см. Пусть О - центр вписанной окружности.
Треугольник COD - прямоугольный, угол СОD - прямой (поскольку ОС и ОВ - биссектрисы углов трапеции C и D, сумма которых равна 180 градусов, значит сумма углов CDO и DCO равна 90 градусов, значит, угол COD = 180 - 90 = 90 градусов). Пусть К - точка касания, тогда ОК - высота прямоугольного треугольника СОD, и к тому же - радиус вписанной окружности. В прямоугольном треугольнике высота к гипотенузе делит теругольник на два, ему подобных. Из подобия тр-ков COK и DOK
СК/ОК = ОК/KD;
4/r = r/25; r = 10;
Ясно, что перпендикулярная основаниям боковая сторона равна диаметру вписанной окружности, то есть АВ = 2*r = 20, сумма боковых сторон равна 4 + 25 + 20 = 49, сумма оснований такая же (раз можно вписать окружность), откуда периметр равен 98, а площадь трапеции равна 98*10/2 = 490.