Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
0,13 м = 1,3 дм
0,73 м = 3,7 дм
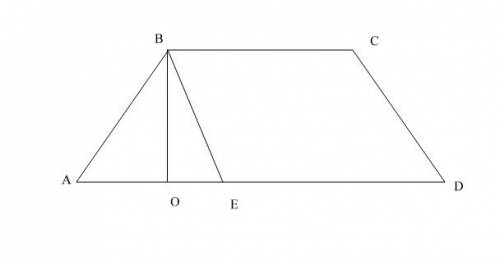
Дана трапеция ABCD, у которой известны все стороны. Нужно найти высоту, чтобы вычислить площадь.
Проведем отрезок BE к нижнему основанию AD параллельно боковой стороне трапеции CD. Поскольку BE и CD параллельны и проведены между параллельными основаниями трапеции BC и DA, то BCDE - параллелограмм, и его противоположные стороны BE и CD равны. BE=CD.
Рассмотрите треугольник ABE. AE=AD-ED. Основания трапеции BC и AD известны, а в параллелограмме BCDE противолежащие стороны ED и BC равны. ED=BC, значит, AE=AD-BC.
Теперь найдем площадь треугольника ABE по формуле Герона (вложение 2).
p = 4,5
S = 2,4
Найдем высоту
ВО = 2S / AE
BO = 0,6
Высота треугольник является и высотой трапеции.
Sтрап = (2+6)*0,6 / 2 = 2,4 дм .
.
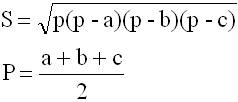
6√3 см
Объяснение:
R6=(a√3)/2=(4√3*√3)/2=2*3=6 cм (R6 - радиус вписанной окр-сти в 6-угольник)
R3=(a√3)/3 (R3 - радиус описанной около треугольника окружности)
a√3=3*R3
a=(3*R3)/√3=(3*6)/√3=(18√3)/3=6√3 см
ответ: 6√3 см