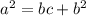
Решение для остроугольного треугольника ( для тупоугольного треугольника решение будет аналогичным )
Объяснение:

ответ: S=90
Объяснение: обозначим коэффициенты 5 и 3 как 5х и 3х. Проведём высоту на нижнее основание трапеции ещё через другую вершину. У нас получилось 2 высоты на нижнем основании, которые образуют на этом основании отрезок равный верхнему основанию и равный 7см. От нижнего основания мы отнимает отрезок 7см: 23-7=16см. Это сумма длин отрезков на нижнем основании по бокам от отрезка 7см. Так как трапеция равнобедренная, то эти боковые отрезки равны. Поэтому 16÷2=8. Каждый боковой отрезок 8см. Высота трапеции вместе с боковой стороной образуют прямоугольный треугольник. Найдём высоту по теореме Пифагора:
(5х)^-(3х)^=8^
25х^-9х^=8^
16х^=64
х^=4
х=2
Теперь найдём остальное, зная х. Боковая сторона =5×2=10см
Высота= 3×2=6см.
Теперь найдём площадь трапеции: S трапеции=( 23+7)÷2×6= 30÷2×6= 15×6=90см
Галочки, которые я обозначила сверху над цифрами в уравнении читайте как в КВАДРАТЕ.
OK и ON- радиусы одной окружности=> они равны=> треугольник NOK- равнобедренный и его углы при основании (угол x и угол KNO) равны. Теперь найдем угол KON. Он смежный с углов MOK, а смежные углы дают в сумме 180 градусов. То есть угол KON= 180-78=102 градуса. Сумма углов треугольника равна 180 градусов. Угол KON+ угол KNO+ угол x= 180 градусов=> угол KNO+ угол x=180- угол KON=180-102=78 градусов. Углы KNO и x равны=> их сумму можно записать как 2KNO или 2x. Получили уравнение: 2x=78, откуда x= 39.
ответ: угол x=39 градусов.
Есть и другой, более рациональный решения:
Угол MOK- внешний для треугольника KON. А внешний угол равен сумме двух внутренних углов треугольника, не смежных с ним => угол KON+ угол x =угол MOK= 78 градусов. Далее, также, как и в доказываем равенство углов KON и x. То есть сумма этих углов будет равна 2x. В итоге получаем то же самое уравнение и, следовательно, тот же самый ответ.
Надеюсь
Применим теорему косинусов для двух углов:
Из данной в условии формулы:
Подставим выражение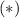 в обе теоремы косинусов:
в обе теоремы косинусов:
Так как нам известно, каким именно образом должны относиться друг к другу углы (А в 2 раза больше), применим формулу косинуса двойного угла для проверки.
Подставим выражение
А это и есть полученый ранее косинус. Значит наше предположение было верно. чтд