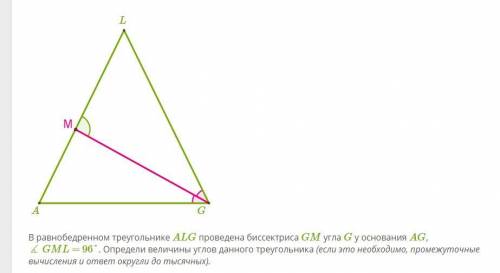
ответ:∠L=52°, ∠A=64°, ∠G=64°
Так как треугольник равнобедренный с основанием AG, то углы при основании равны
∠A=∠G =х
А ∠ GML - внешний угол Δ AМG
∠ GML =∠А+1/2∠ G;
х+1/2 х=96°;
х=96° : 3/2;
х=64°- величина углов∠Aи∠G
По теореме о сумме трёх углов треугольника :
∠L=180°-2∠A=180°-2*64°=52°
a) 100°; 40°; 40°.
б) 90°; 45°; 45°.
в) 50°; 65°; 65°.
Объяснение:
По теореме о сумме углов треугольника (сумма внутренних углов треугольника равна 180°).
В равнобедренном треугольнике углы при основании равны.
a) Значит, два угла при основании равны по 40°. Сумма углов при основании равна
40° + 40° = 80°
Зная это, найдем третий угол (при вершине):
180° - 80° = 100 (градусов) - угол при вершине.
б) Значит, на углы при основании остаётся:
180° - 90° = 90°
Так как они равны в равнобедренном треугольнике:
90° : 2 = 45 (градусов) - величина каждого угла при основании.
в) Значит, на углы при основании остаётся:
180° - 50° = 130°
Так как они равны в равнобедренном треугольнике:
130° : 2 = 65 (градусов) - величина каждого угла при основании.
Объяснение:
Выясним, какой должна быть гипотенуза в нашем треугольнике, когда из условия задачи нам известно, что длины катетов этого треугольника равны 7 и 24 сантиметрам:
√(72 + 242) = √(49 + 576) = √625 = 25.
Выясним, каким тогда будет радиус описанной окружности, ведь мы знаем, что она соответствует половине гипотенузы:
25 : 2 = 12,5.
Выясним, каким тогда будет радиус вписанной окружности:
(7 + 24 - 25) : 2 = 3.
ответ: При таких начальных условиях радиус вписанной будет равен 3 см, а радиус описанной 12,5 см.
Биссектриса MG — делит угол G пополам.
Объявим <A & <MGA — как переменные: <A = 2x; <MGA = x.
<AMG = 180-96 = 84°.
Сумма углов треугольника равна 180°, тоесть, уравнение таково:
Вывод: <L = 52°; <A == <G = 64°.