а) Возьмем угол С прямой. Получим теорему Пифагора, косинус прямого угла равен нулю. а=3, в=4, с=5.
Можно взять угол С тупой, тогда срабатывает теорема косинусов, при условии выполнения неравенства треугольников такой треугольник будет существовать.
ответ Существует.
б) Отношение а к с равно отношению косинуса А к косинусу С. Возьмем, например, угол А и угол С по 45°, а угол В прямой. Тогда при выполнении неравенства треугольников такой треугольник прямоугольный равнобедренный существует.
в) Если угол В прямой, а угол А равен 30°,
сторона с =а√3, в=2а
ответ Существует
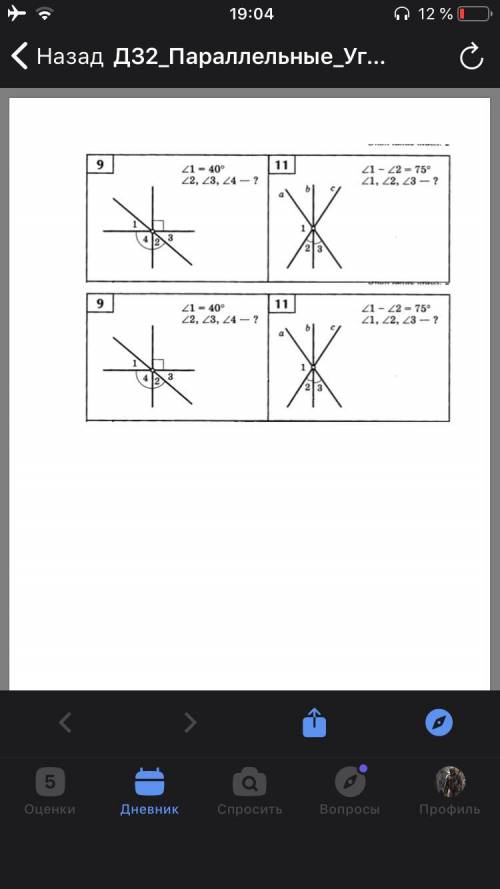
угол 4 = 90°, т.к. он и угол, обозначенный квадратиком являются вертикальными, а вертикальные углы равны ( они образуются при пересечении двух прямых)
по аналогии угол 1 = углу 3 = 40°
угол 4 + угол 2 + угол 3 образуют развёрнутый угол, который равен 180°. Мы знаем угол 4 и 3. Тогда угол 2 = 180° -90° - 40° = 50°