Площадь трапеции равна 900√3 м²
Объяснение:
Дано:
ABCD - трапеция
АС - диагональ трапеции
AB = CD - боковые стороны
АС ⊥ CD
AD = 40√3 м - большее основание
∠A = ∠D = 60°
Найти:
S - площадь трапеции
Рассмотрим прямоугольный треугольник ACD, гипотенуза которого AD = 40√3 м и ∠D = 60°.
Катеты АС и CD этого треугольника равны
АC = AD · sin 60° = 40√3 · 0.5√3 = 60 (м)
CD = AD · cos 60° = 40√3 · 0.5 = 20√3 (м)
Поскольку трапеция равнобедренная, то
АВ = CD = 20√3 м.
Из вершины С прямого угла треугольника ACD опустим на гипотенузу AD высоту CK, которая одновременно является и высотой трапеции
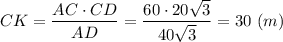
В треугольнике ACD
∠CAD = 90° - ∠D = 90° - 60° = 30°
Основания трапеции ВС ║ АD
∠ACB = ∠CAD = 30° (внутренние накрест лежащие углы при ВС ║ АD и секущей АС).
Рассмотрим ΔАВС.
∠ВАС = ∠BАD - ∠CAD = 60° - 30° = 30°
Поскольку в ΔАВС углы ∠ВАС = ∠ACB = 30°, то ΔАВС - равнобедренный, то есть ВС = АВ = 20√3 м.
Площадь трапеции равна произведению полусуммы оснований на высоту.
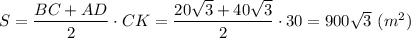
Подобные задачи встречаются довольно часто, как по отдельности, так и пакетом. .
1) Через точку пересечения диагоналей квадрата MNPQ (точку О) проведён перпендикуляр OD к его плоскости. OD=8см, MN=12см.
Вычислите:
а) расстояние от точки D до прямой NP.
б) площади треугольника MDN и его проекции на плоскость квадрата.
в )расстояние между прямыми OD и MN
Решение:.
Вспомним, что диагонали квадрата равны, пересекаются под прямым углом и точкой пересечения делятся пополам.
а) Расстояние от точки до прямой - длина отрезка, проведенная перпендикулярно из точки к прямой. Расстояние от D до прямой NP - наклонная DH, проведенная перпендикулярно NP.
По т.о 3-х перпендикулярах ОН⊥MP; DH ⊥NP⇒
ОН=КN=MN:2=6 см
⊿ DOH - египетский - это следует из отношения его катетов ОН:OD=3:4; его гипотенуза DH=10 см- это и есть искомое расстояние. ( можно проверить по т.Пифагора).
б) Расстояния от D до каждой из сторон и от ОD до каждой из вершин квадрата соответственно равны, т.к. DO проецируется в центр основания, О - центр вписанной ( и описанной) окружности ⇒ ОК=ОH=6 см
∆ MDN- равнобедренный, его высота DK=DH=10 см
S (∆ MDN)=DK•KN=10•6=60 см²
Проекция ∆ MDN на плоскость квадрата - это прямоугольный ∆ MON. Его основание МN - общее с ∆ MDN, вершина D ∆ MDN проецируется в точку пересечения диагоналей, образующих прямой угол, ОM=ON как половины диагоналей квадрата.
MN=12 см, высота ОК=6 см
S (∆ MON)=OK•MN:2=36 см²
в)
DO и MN- скрещивающиеся прямые, расстояние между ними определяется общим перпендикуляром ОК, а так как он равен половине длины стороны квадрата (см. выше), то это расстояние равно 6 см.
––––––––––––
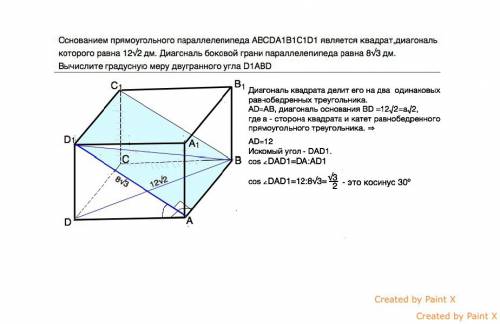
2) Основанием прямоугольного параллелепипеда ABCDA1B1C1D1 является квадрат, диагональ которого равна 12√2 дм. Диагональ боковой грани параллелепипеда равна 8√3 дм.
Вычислите градусную меру двугранного угла D1ABD
--------------------
Решение здесь несложное и короткое, в отличие от пояснения.
Сделаем рисунок.
Двугранный угол, градусную меру которого нужно вычислить, составлен плоскостью ∆ D1АВ и плоскостью ∆ DАВ. Первый лежит в плоскости диагонального сечения параллелепипеда, второй - в плоскости квадрата, его основания.
Величина двугранного угла равна его линейному углу, который образован двумя лучами, проведенными в каждой из плоскостей перпендикулярно одной точке на линии их пересечения.
АD1⊥АВ, АD⊥АВ⇒ искомый угол - угол D1АD.
Диагональ квадрата делит его на два равнобедренных прямоугольных треугольника. АD=АВ, и ВD =12√2
АD можно найти
а) по т.Пифагора;
б) через синус (косинус) 45º или
просто вспомнить, что диагональ квадрата ( как и гипотенуза равнобедренного прямоугольного треугольника) равна а√2, где а - сторона квадрата или катет равнобедренного прямоугольного треугольника. ⇒
АD=12
cos ∠DAD1=DA:AD1
cos ∠DAD1=12:8√3=(√3):2 - это косинус 30º - искомого угла.