У ∆АВС відомо, що АС=6 см, ∠А = 80˚, ∠С = 40˚. Знайти радіус кола, описаного навколо трикутника. Я вас очень , объясните как решать НЕ ЧЕРЕЗ ТЕОРЕМУ СИНУСОВ, А ВЫРАЗИТЬ СРАЗУ
1) Из прямоугольного труугольника, сторонами которого являются сторона основания и половины диагоналей по т. Пифагора находим сторону основания : С боковым ребром диагональ боковой грани образует угол 90-60=30°, значит диагональ боковой грани в два раза больше стороны основания, т. е 34 см По т. Пифагора находим боковое ребро : Площадь боковой поверхности призмы равна:
2) Найдём площадь основания призмы (площадь Δ-ка), применив формулу Герона (мою любимую ))))) ): , где - полупериметр, - стороны.
Находим боковое ребро :
Как-то так...
...Ну и как "Лучший ответ", я надеюсь, не забудешь отметить, ОК?!.. ;)
а) Точка пересечения прямых находится совместным решением уравнений прямых: y=3x-1 и x-3y+1=0Выразим их в виде системы: 3х - у = 1 3х - у = 1 х - 3у = -1 -3х + 9у = 3 8у = 4 у = 4/8 = 0,5 х = -1 + у = -1 + 3*0,5 = -1 + 1,5 = 0,5 Точка пересечения (0,5; 0,5).
б) Угол между прямыми : две неперпендикулярные прямые A1, A2 (взятые в данном порядке) представляются уравнениями y=a1x+b1, y=a2x+b2. Тогда формула для определения угла между ними: . У первой прямой коэффициент а1 = 3 Для второго надо уравнение выразить относительно у: . а2 = 1/3. Тангенс угла равен: . Данному тангенсу соответствует угол -53.1301 градуса. Знак минус означает, что вторая линия имеет меньший угол наклона к оси х. В этом можно убедиться по коэффициентам а в уравнении прямой у = ах + в. Коэффициент а равен тангенсу угла наклона прямой к оси х. а1 = 3. α1 = arc tg 3 = 71.56505 градус. a2 = 1/3 α2 = arc tg(1/3) = 18.43495 градус. Если отнять 18.43495 - 71.56505 = -53.1301 градус.
Есть такое свойство в произвольном треугольнике, что точка пересечения серединных перпендикуляров — это центр описанной окружности.
Тоесть, если мы проведём с этого центра отрезок до какой-то вершины треугольника — то этот отрезок будет равен радиусу описанной окружности.
HC == BH == AH = R.
<A = 80°; <AFH == <AEH = 90° ⇒ <FHE = 360-(90+90+80) = 100°.
<FHE = 100° ⇒ <EHC = 180-100 = 80°.
<EHC = 80°; <HEC = 90° ⇒ <HCE = 90-80 = 10°.
AC = 6.
AE == EC = AC/2 ⇒ AE == EC = 6/2 = 3.
EC = 3; <HCE = 10°(α), тоесть — по теореме тангенсов:
Как я говорила, отрезок, проведённый с вершины треугольника до центра описанной окружности — равен радиусу, тоесть: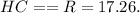
Вывод: R = 17.26.