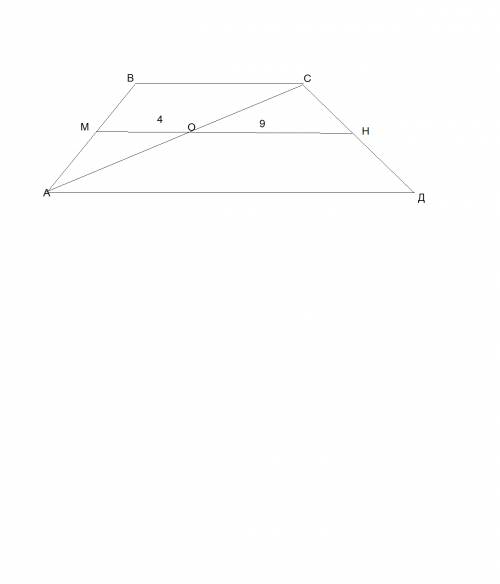
Длина средней линии трапецыи становит 4+9=13см. Отсюда мы можем найти суму основ трапецыи, за формулой про нахождения средней линии трапецыи (средняя линя равняеться полсуме основ- (ВС+АД)/2=МН), отсюда ВС+АД=13*2=26см.
Расмотрим треугольник АВС, у него: диагональ АС делит среднюю линию на две равных части, отсюда МО-средняя линия этого треугольника, а значит она равна половине линии, которая ей лежит паралельно(линии ВС)=4*2=8см.- это меньшее основание, теперь мы можем найти большее основание: 26-8=18см.
ответ:8см., 18см.
130°
Объяснение:
Так как O - центр вписанной окружности, а этот центр, напомню, лежит на точке пересечения биссектрис, то биссектрисы BL и AK (мы их сами построили) проходят через него. Тогда угол ABO = 30, угол BAO = 20. Значит, угол AOB = 180 - 20 - 30 = 130°.