Тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему.
Прилежащий катет ВС = 5 см, противолежащий катет АС = АВ-1, АВ - гипотенуза.
AC² = AB²-BC² = (AC+1)²-5² = AC²+2AC+1-25
2AC=24
AC=12
tg b = AC/BC = 12/5 = 2,4
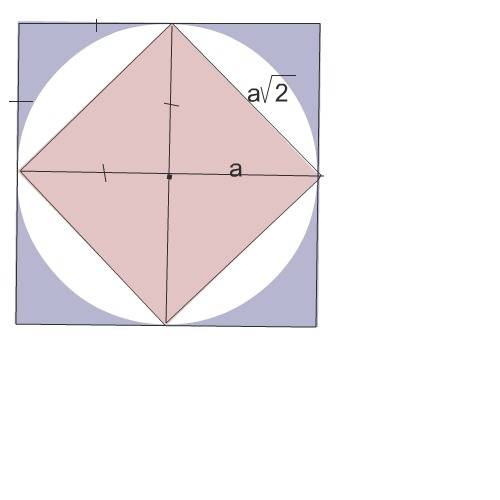
Задачу можно решить с чертежа ( графически). См. рисунок.
По нему понятно, что описанный квадрат состоит из 4-х равных квадратов со стороной=а:2
Вписанный квадрат состоит из 4 прямоугольных треугольников, каждый из которых равен половине одного квадратика описанного квадрата.
Отсюда: Площадь квадрата вписанного в круг, меньше площади квадрата,описанного около этого круга, в 2 раза.
2-й вариант решения.
Пусть сторона вписанного квадрата будет а, а его диагональ - d
Тогда его площадь равна
S₁=a²
Сторона описанного квадрата равна диагонали d вписанного в эту же окружность квадрата и равна
d=а√2
Площадь этого квадрата
S₂ =d²=(а√2)=2а²
S₂:S₁=2а²:а²=2
Пусть АС=х см, то АВ=х+1 см, тогда по т. Пифагора AB^2=BC^2+AC^2
(x+1)^2=25+x^2
2x=24
x=12
Значит АС=12 см, АВ=13см, tgB=AC/BC=12/5