(см. объяснение)
Объяснение:
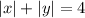
Перед нами уравнение квадрата, точка пересечения диагоналей которого имеет координаты (0; 0) и расстояние от точки пересечения диагоналей которого до одной из вершин равно 4.
Зная это, построим график:
(см. прикрепленный файл)
Задание выполнено!
Комментарий 1:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой: либо y=-x+4, либо y=-x-4, либо y=x-4, либо y=x+4. Строим их до пересечения, таким образом получая график.
Комментарий 2:
Функция непрерывна и при любом раскрытии модуля будет получаться уравнение прямой, причем точки "склеивания" будут в координатах (0; 4), (4; 0), (-4; 0), (0; -4). Тогда соединим их и получим график.
Комментарий 3:
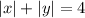
При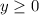 
получим график модуля 
.
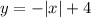При 
будет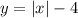 
.
Строим это и получаем график.
Линейный угол двугранного угла - это угол, образованный двумя лучами, которые имеют общее начало, лежащее на ребре двугранного угла, и проведенными в обеих гранях перпендикулярно этому ребру.
Обе плоскости сечения содержат в себе диагональ куба А1С, которая является линией их пересечения.
Соотношение линейных величин у кубов одинаковы.
Пусть данный куб единичный, где его ребро равно 1.
Тогда его диагональ А1С по формуле диагонали куба равна √3, а диагональ его грани равна √2.
А1С=√3 А1В=√2
Искомый угол ∠В1КН, где В1К - высота треугольник аА1В1С.
В1Н - перпендикуляр из В1 на плоскость А1СВ, в частности, В1Н перпендикулярен А1В.
Из треугольник аА1В1С найдем В1К.
Треугольники А1В1С и КВ1С подобны.
А1В1:В1К=А1С:В1С
1/В1К=√3/√2
Грани куба - равные квадраты.
Диагонали квадрата перпендикулярны и точкой пересечения делятся пополам.
В1Н ⊥ А1В, ⇒ является половиной диагонали грани куба и равна ( √2):2
В1К ⊥ А1С, НК ⊥ А1С.
Треугольник В1НК - прямоугольный.
cos ∠ НВ1К=В1Н:В1К
cos ∠НВ1К=(√2/2):√2/√3=√3/2, и это косинус угла 30º.
Значит, угол В1КН, как второй острый угол прямоугольного треугольника, равен 90º-30º=60º