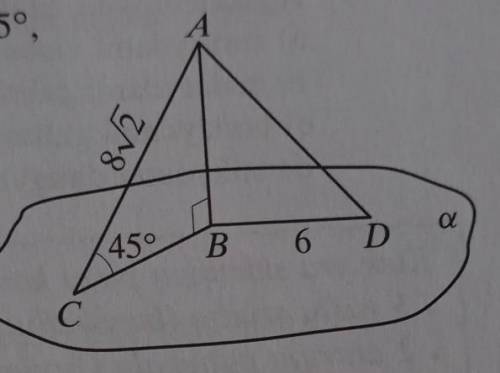
Дано :
a ║ b.
c - секущая.
∠1 = 102°.
Найти :
Меньший угол = ?
При пересечении двух параллельных прямых секущей накрест лежащие углы равны, соответственные углы равны, сумма односторонних углов равна 180°.∠1 и ∠8 - внешние односторонние.
По выше сказанному -
∠1 + ∠8 = 180°
∠8 = 180° - ∠1 = 180° - 102° = 78°.
∠1 = ∠5 = 102° (соответственные при параллельных прямых)
∠4 = ∠8 = 78° (соответственные при параллельных прямых)
∠5 = ∠3 = 102° (внутренние накрест лежащие при параллельных прямых)
∠3 = ∠7 = 102° (соответственные при параллельных прямых)
∠6 = ∠8 = 78° (вертикальные)
∠2 = ∠4 = 78° (вертикальные).
Самый меньший угол, который образовался, равен 78°.
78°.
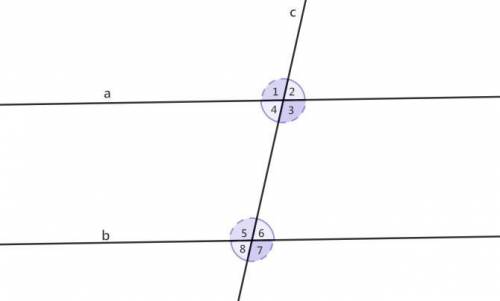
V=312√3π(см³)
Объяснение:
осевым сечением цилиндра является прямоугольник. Обозначим его вершины А В С Д ч диагоналями АС и ВД, точку их пересечения К, а высоту ОО1. Объем цилиндра вычисляется по формуле: V=Sосн×ОО1, где основанием является окружность. Диагонали сечения пересекаясь делятся пополам поэтому АК=КС=ВК=ВД=10÷2=5см
Рассмотрим полученный ∆АКД. Он равнобедренный и <А=<Д=(180–60)÷2=120÷2=60°
Итак: ∆АКД- равносторонний, поскольку все его углы равны, и каждый составляет 60°, поэтому АК=КД=АД=5см.
Вычислим площадь сечения АВСД по формуле:
S=сеч½×AC²×sin60°=½×10²×√3/2=½×100×√3/2=
=25√3см²
Sсеч=25√3см²
Зная площадь сечения найдём высоту ОО1:
ОО1=Sсеч÷АД=25√3÷5=5√3см; ОО1=5√3см
Радиус АО1=О1Д=АД÷2=5÷2=2,5 см
Sосн=πr²=π×(2,5)²=6,25π
Теперь найдём объем цилиндра зная его площадь основания и высоту:
V=Sосн×ОО1=6,25π×5√3=312√3π(см³)
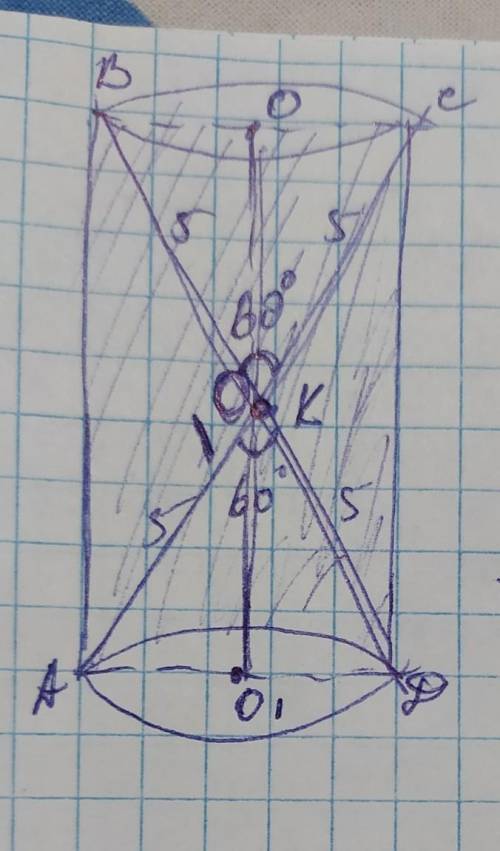
АD=10
Объяснение:
СВ=АВ, треугольник ∆АСВ- равнобедренный ( <АВС=90°; <АСВ=45°, по условию; <САВ=90°-45°=45°.)
Углы при основании равны.
АВ=СА/√2=8√2/√2=8 ед
∆ABD- прямоугольный треугольник
Теорема Пифагора
АD=√(AB²+BD²)=√(8²+6²)=√(64+36)=√100=
=10 ед