
4. т.к. АВ∠ВС∠АС, то С∠А∠В (по теореме о сторонах и углах треугольника)
180-(110+50)=20 (т.к. сумма углов в треугольнике равна 180)
∠С=110
∠А=50
∠В=20
5.
1)пусть х-основание
тогда х+15-боковая сторона
х+15+х+15+х=48
3х=48-30
3х=18
х=6-основание
х+15=21-боковые стороны (таких две, и они авны, т.к. треугольник равнобедренный)
2)пусть х-боковая сторона
тогда х+15-основание
х+х+х+15=48
3х=33
х=11-боковая сторона
х+15=26-основание
6. т.к. угол ВАН=35, то угол НВА=90-35=55 (по первому св-ву прямоугольного треугольника)
угол АВС=180-55=125, как смежный
угол ВАС=180-(125+25)=30 (т.к. сумма углов в треугольнике равна 180)
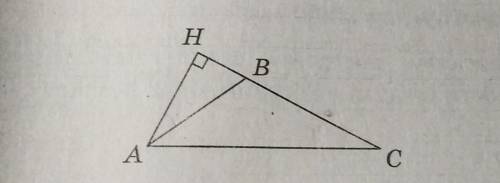
Смотрите на фотографиях