в равнобедренном треугольнике биссектриса,проведённая к основанию является медианой и высотой.
доказательство.:
рассмотрим рисунок ABC-равнобедренный треугольник с основанием BC,AD-его биссектриса.
Из равенства треугольников ABD и ACD следует что BC=DC и угол 3= углу 4. Равенство BC=DC означает что точка D-середина стороны BC и поэтому AD-медиана треугольника ABC. т.к угла 3 и 4-смежные и равны друг другу ,то они прямые. Следовательно , отрезок AD является также высотой треугольника ABC. Теорема доказанна.
1. У правильных многоугольников все стороны и углы равны. Пермиетр правильного треугольника по стороне а: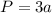
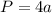
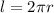. Тогда, из простейших геометрических соображений, длина дуги l1 будет равна: 
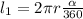, где α - центральный угол.
Правильного четырехугольника:
2. Вся окружность соответствует центральному углу в 360 градусов. Очевидно, если мы возьмем половину окружности, то угол так же поделится надвое, а длина дуги будет составлять половину длины окружности. Так же будут относиться и площади.
Длина окружности:
a)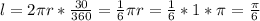
б)