Обозначим длину окружности L. L=2*PI*R(1). Периметр n - угольника (Рn) = длина стороны (An) * кол-во сторон (n). Кол-во сторон нам известно. Надо выразить An через длину окружности. По формуле An=2*R*sin(180/n). Из (1) формулы выражаем радиус: R=L/(2*PI). Подставляем её в формулу: An=2*sin(180/n)*L/(2*P)=sin(180/n)*L/PI. Теперь подставляем всё это в формулу периметра: Pn=n*sin(180/n)*L/PI. Вот формула, как найти периметр n - угольника.
Пример для 6 - угльника:
P6=6*sin30*L/PI=3*L/PI. А дальше всё просто: подставляешь значение длины окружности и значение PI и получаешь ответ.
//PI - число ПИ.
Будем считать, что задание дано так:
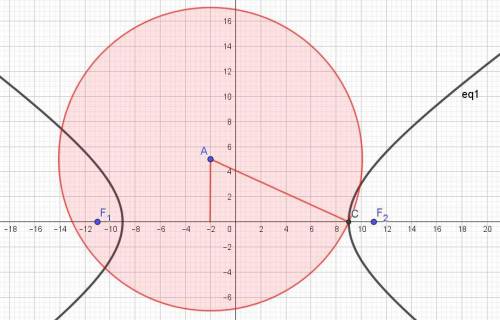
Определить уравнение окружности, проходящей через правую вершину гиперболы 40x² - 81y² = 3240 и имеющей центр в точке А(-2; 5).
Уравнение гиперболы приведём к каноническому виду, разделив обе части заданного уравнения на 3240:
(x²/81) - (y²/40) = 1.
Или так: (x²/9²) - (y²/(2√10)²) = 1 это и есть каноническое уравнение.
Отсюда находим координаты правой вершины гиперболы: С(9; 0).
Теперь находим радиус заданной окружности как отрезок АС.
АС = √((9 - (-2))² + (0 - 5)²) = √(121 + 25) = √146.
Получаем ответ: (x + 2)² + (y - 5)² = 146.
для 7-угольника:Р=7t
t=сторона семиугольника
для 6-угольника:Р=6t
t=сторона семиугольника
для 5-угольника:Р=5t
t=сторона семиугольника