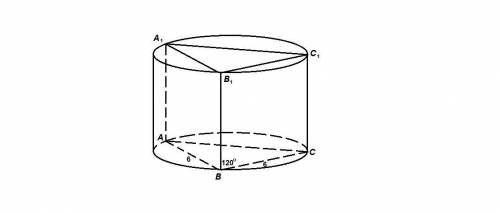
Прямая призма АВСА₁В₁С₁ вписана в цилиндр. АВ = ВС = 6, ∠АВС = 120°, АА₁ = 10.
Найти площадь боковой поверхности цилиндра.
ответ: 120π
Объяснение:
Если прямая призма вписана в цилиндр, то высота цилиндра равна длине бокового ребра призмы:
Н = АА₁ = 10,
а основания цилиндра описаны около оснований призмы.
ΔАВС равнобедренный, тогда
∠А = ∠С = (180° - 120°)/2 = 30°
Радиус окружности, описанной около треугольника, можно найти по формуле:
R = AB / (2 sin∠C) = 6 / (2 · 1/2) = 6
Площадь боковой поверхности цилиндра:
Sбок.цил. = 2πR · H = 2π · 6 · 10 = 120π кв. ед.
Объяснение:
1) Правильная пирамида - это такая пирамида, в основании которой лежит правильный многоугольник, а высота проецируется в центр основания.
2) Правильным называется многоугольник, у которого все стороны и углы одинаковые. Согласно этому определению, ромб не является правильным многоугольником (не соответствует критерию равенства всех углов).
3) Следовательно, в отношении такой пирамиды не применима формула расчета площади боковой поверхности через площадь основания и cos α - угла между апофемой боковой грани и её проекцией на плоскость основания.