<А=<С=120°, <В<Д=60°
Объяснение:
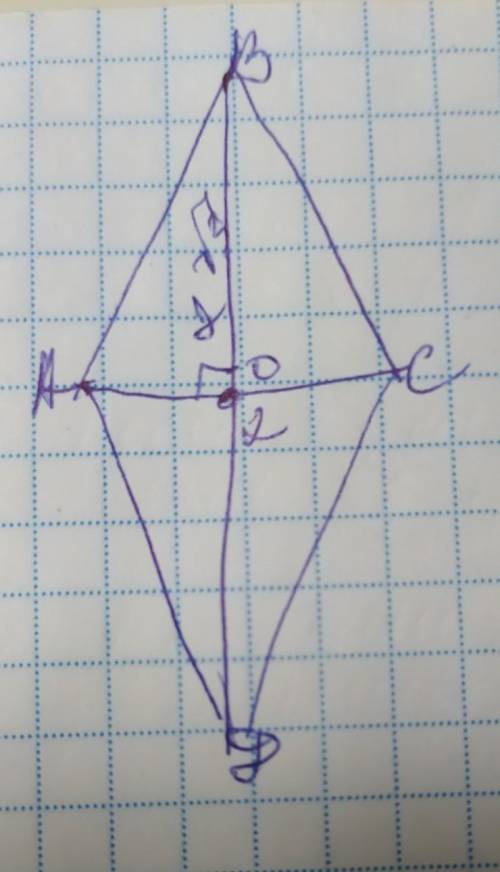
обозначим вершины ромба А В С Д с диагоналями АС и ВД а точку их пересечения О. Диагонали ромба пересекаясь делятся пополам под прямым углом, образуя 4 равных прямоугольных треугольника, а также противоположные углы ромба равны и диагонали при пересечении делят углы из которых они проведены, пополам, поэтому АО=СО=2÷2=1см, ВО=ДО=2√3÷2=√3см
Теперь найдём угол через тангенс угла АВО. Тангенс угла - это отношение противолежащего от
угла катета к прилежащему:
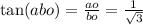
tg 1/√3=30°- это половина угла В,
Тогда <В=<Д=30×2=60°
Сумма углов ромба, прилегающие к одной стороне, составляет 180°, поэтому <А=<С=180–60=120°
обращаю внимание что 1/√3=√3/3, поскольку 1/√3 - это сокращённая дробь от √3/3. В тригонометрической таблице указано именно √3/3
I випадок
Дано: ∆АВС - рівнобедрений, АС = 20 см, АС - основа, AN - медіана.
P∆АВN > P∆ANC на 6 см.
Знайти: АВ.
Розв'язання:
Нехай CN = х см.
Якщо за умовою AN - медіана, тоді BN = NC = 1/2ВС.
Отже, BN = NC = х см, тоді АВ = ВС = 2х (см).
P∆ANC = AN + NC + AC.
P∆ANC = AN + х + 20; P∆ANВ = AN + BN + АВ
P∆ANВ = AN + x + 2x = 3x + AN.
За умовою P∆ANС < P∆ANВ на 6 см, тоді P∆ANВ - P∆ANC = 6.
(3х + AN) - (AN + x + 20) = 6; 3x + AN - АN - x - 20 = 6; 2x - 20 = 6;
2x = 6 + 20; 2x = 26; x = 26 : 2; x = 13. Тоді АВ = 2 • 13 = 26 (см).
II випадок
Дано: ∆АВС- рівнобедрений, АС = 20 см, АС - основа, AN - медіана,
P∆АВN > P∆ANC на 6 см. Знайти: АВ.
Розв'язання:
Аналогічно I випадку маємо Р∆ANC = AN + х + 20;
Р∆АВN = 3x + AN.
За умовою Р∆АNС > Р∆АВN, на 6 см, тоді Р∆АNС > Р∆АВN = 6.
(AN + х + 20) - (3х + AN) = 6; AN + x + 20 - 3x - AN = 6; 20 - 2х = 6;
-2х = 6 - 20; -2х = -14; х = 7. Тоді АВ = 2 • 7 = 14 (см).
Biдповідь: 26 см або 14 см.
Объяснение: