1) Сумма внешнего и внутреннего угла многоугольника равна 180° ⇒ следовательно внутренний угол многоугольника равен 180° - 20° = 160°
Величина внутреннего угла правильного многоугольника зависит от количества его сторон n и выражается формулой:
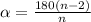
Найдем при каком n угол будет равен 160°:
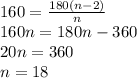
Т.е. угол в 160° будет у правильного 18-угольника
2) Радиус окружности описанной около правильного треугольника R и сторона a треугольника связаны соотношением:
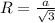
Подставим заданное значение стороны:
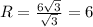
Следовательно, радиус окружности, описанной около этого треугольника равен 6 см
3) Градусная мера всей окружности равна 360°, а радианная мера 2π, следовательно градусная мера дуги равна:
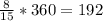 °
°
а радианная:

Длину дуги найдем как 8/15 от длины окружности:
 см
см
B, C - точки касания
OB=OC =4,5 (радиусы)
Радиус в точку касания перпендикулярен касательной, ∠OBA=∠OCA=90°
△AOB=△AOC (по катету и гипотенузе) => ∠BAO=∠CAO
Доказали: касательные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
OB/OA =4,5/9 =1/2
В треугольнике AOB катет OB равен половине гипотенузы OA, следовательно лежит против угла 30°.
∠BAO=30° => ∠BAC =30*2 =60°