Если коэффициент пропорциональности х, то меньший угол 2х, а больший 3х. Их сумма 2х+3х=90, откуда х=90/5; х= 18, значит, больший угол равен 18°*3=54°
ответ 54°
2. Т.к. АС=ВС, то по определению равнобедренного треугольника ΔАВС равнобедренный с основанием АВ, тогда углы при основании АВ равны, угол В равен 40°, а угол С равен 180°-(∠А+∠В)=180°-(40°+40°)=100°
ответ 100°
3. Углы А и В в ΔАВС равны по свойству углов при основании в равнобедренном треугольнике. Поэтому угол А равен
(180град. -120град.)/2=30 град.
ответ 30 градусов
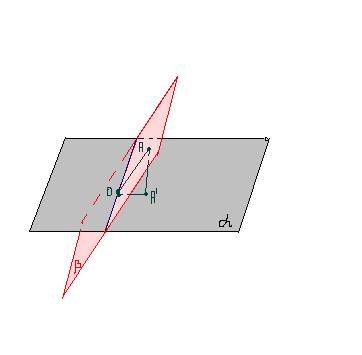
Итак, что мы имеем? 2 пересек. плоскости, а (альфа )(серая) и b (бета) (розовая).
Линия их пересечения обозначена синим.
Точка A' является проекцией точки А на плоскость а. Значит, угол AA'O=90* (градусов)))
Также линия пересечения плоскостей (синяя) образует прямые углы с OA' и с ОА. (Правило какое-то есть, правило 3х перпендикуляров, кажется, или что-то типа того. Поройся в учебнике, обязательно найдешь)))
Рассмотрим прямоугольный треугольник AA'O. Угол AA'O=90*. ОА=14, OA'=7. ОA' - катет, ОА - гипотенуза. И ОA'=ОА/2. Катет, лежащий напротив угла в 30*, равен половине гипотенузы. (Помнишь?))) Следовательно, угол ОАA'=30*. Сумма углов треугольника 180*. Значит, угол АОA'=60*. А это и есть угол между плоскостями.
2.
a(2;0;-1)
b(3;-1;2)
Вычислим координаты векторов b-a и 2a-rb:
b-a(1;-1;3)
2a-rb(4-3r;r;-2-2r)
Далее, эти векторы перпендикулярны, следовательно, их скалярное произведение должно быть равно 0.
Скалярное произведение векторов равно сумме произведений координат. Найдем его.
(b-a)*(2a-rb)=4-3r-r-6-6r=-10r-2.
Приравняем к нулю.
-10r-2=0
r=-1/5.
Відповідь:
(0:16)
Пояснення: