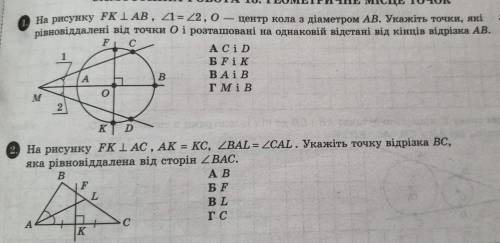

ABCD - правильный тетраэдр, поэтому все его грани это правильные треугольники.
K - середина AC; KD = KB как медианы в равных и правильных треугольниках. KM⊥DB т.к. в равнобедренном треугольнике (ΔDKB), медиана опущенная на основание это и высота.
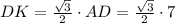 как высота в правильном треугольника.
как высота в правильном треугольника.
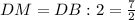
Найдём неизвестный катет в прямоугольном ΔDMK:
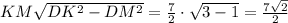
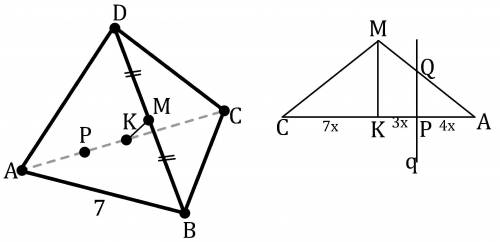
Рассмотрим ΔAMC: K, P∈AC; P∈q║KM; q∩AM=Q.
ΔMKA~ΔQPA по трём углам т.к. PQ║KM.
AK=KC - по условию. Пусть AK = 7x ⇒ AC = 14x.
CP:PA=10x:4x=5:2 ⇒ AP:AK=4x:7x=4:7, коэффициент подобия.
Найдём PQ через подобие треугольников.
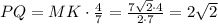
ответ: 2√2.
Про точку P: по условию P может так же лежать между С и K, но ответ будет тем же т.к. точка P не влияет на длину KM, и коэффициент подобия не изменится, только он будет для других треугольников.
ДОКАЗАТЬ: ЕF = BO , EF перпендикулярен АС.
________________________
ДОКАЗАТЕЛЬСТВО:
1) Рассмотрим ∆ BCD:
CF = FD , CE = EB → поэтому EF - средняя линия. По свойству средней линии:
Средняя линия параллельна третьей стороне, то есть BD и равна её половине →
EF || BD и EF = 1/2 × BD
По свойству ромба:
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам →
ВD перпендикулярен АС ; ВО = ОD = 1/2 × BD ; AO = OC = 1/2 × AC
Значит, EF = 1/2 × BD = 1/2 × 2 × BO = BO
2) Как было сказано вышe:
EF || BD, но AC перпендикулярен BD.
Если одна из двух параллельных прямых a или b перпендикулярна третьей прямой c, то и другая прямая a или b перпендикулярна этой же прямой c.
Из этого следует, что EF перпендикулярен AC, что и требовалось доказать.