
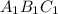 - его проекция на плоскость P.
- его проекция на плоскость P. 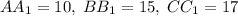 .
.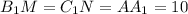 дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.
дм. Тогда BM = 15-10 = 5 дм, CM = 17-10 = 10 дм.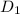 . Этот перпендикуляр разделит отрезок NM пополам. Значит
. Этот перпендикуляр разделит отрезок NM пополам. Значит 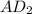 медиана треугольника
медиана треугольника 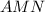 .
.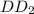 - средняя линия трапеции BCNM. Его длина
- средняя линия трапеции BCNM. Его длина 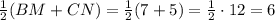 дм.
дм.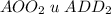 подобны по первому признаку:
подобны по первому признаку:  - общий,
- общий, 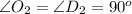 .
.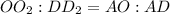
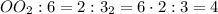 дм.
дм.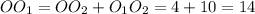 дм.
дм.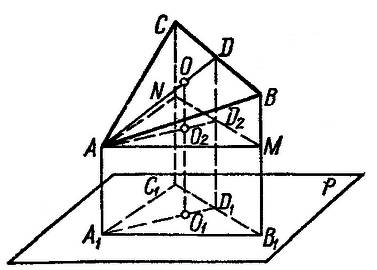
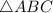 . Из условия ясно, что он — прямоугольный (так как
. Из условия ясно, что он — прямоугольный (так как 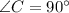 ).
). 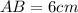 — гипотенуза,
— гипотенуза, 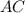 — искомый катет,
— искомый катет, 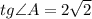
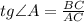
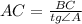
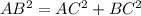
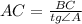 .
.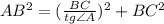
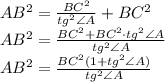
 :
: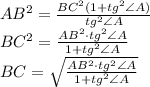
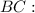
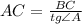
 новую подстановку:
новую подстановку: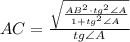
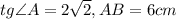
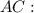
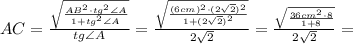
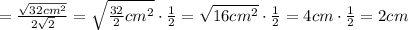

<А=28
Объяснение:
20+32х+4+4+6х=180
38х+28=180
38х=180-28
38х=152
Х=4
<А=4+6х=4+6×4=4+24=28