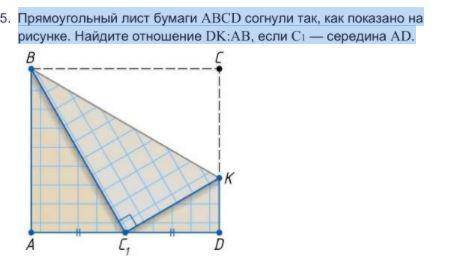
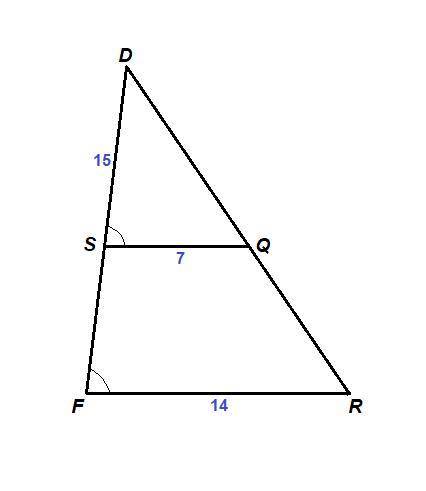
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно. Найди длину стороны DR, если площадь треугольника DSQ равна 42 см², SQ = 7 см, DS = 15 см, FR = 14 см.
4√37 см
Объяснение:
∠DSQ = ∠DFR как соответственные при пересечении SQ║FR секущей DF, ∠D - общий для треугольников DSQ и DFR, значит
ΔDSQ ~ ΔDFR по двум углам.
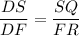
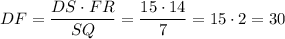 см
см
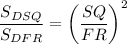
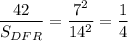
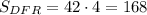 см²
см²
Площадь треугольника DFR можно вычислить так же по формуле:
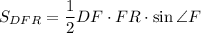
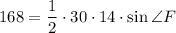
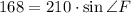
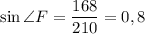
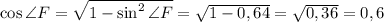
Из треугольника DFR по теореме косинусов:
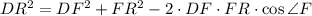
DR² = 30² + 14² - 2 · 30 · 14 · 0,6
DR² = 900 + 196 - 504 = 592
DR = √592 = 4√37 см
все на фото ...........