AC:16=7:3––АС=16•7:3=28 см
Объяснение:
Примем коэффициент отношения отрезков на АВ равным а,Так как AM : MB = 3:4, то АВ=АМ+ВМ=7а ⇒ AM:AB = 3:7.
CN:CB = 3:7- дано.
а) Точки М и N лежат в плоскости ∆ АВС и в плоскости α. ⇒MN - линия пересечения этих плоскостей.
МN и АС высекают на прямых АВ и ВС пропорциональные отрезки.
Из обобщённой теоремы Фалеса: если отрезки, высекаемые прямыми на одной прямой, пропорциональны отрезкам, высекаемым теми же прямыми на другой прямой, то эти прямые параллельны.⇒ АС║MN.
Если прямая (АС), не лежащая в плоскости α, параллельна некоторой прямой (MN), которая лежит в плоскости α, то прямая параллельна плоскости . ⇒АС || α
б) Т.к. MN║AC, углы при их пересечении секущими АВ с одной стороны и ВС с другой равны как соответственные. Отсюда следует подобие треугольников MBN и ABC с коэффициентом подобия k=BC:NC=7:3 ⇒ AC:MN=7:3
AC:16=7:3––АС=16•7:3=28 см
Дано: ΔАВС, АВ=1 см, АС=8 см, ∠А=60°. Найти ВС.
По теореме косинусов
ВС²=АВ²+ВС²-2*АВ*ВС*сos60=1+64-2*1*8*1/2=65-8=57
ВС=√57≈7,55 см

8
Объяснение:
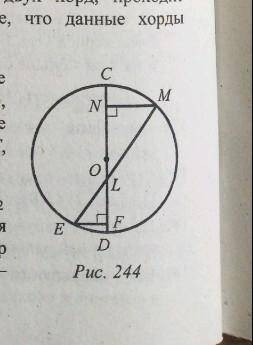
ΔLMN≅ΔLEF по двум углам: ∠ELN=∠MLN как вертикальные и ∠LNO=∠LFE=90°
У подобных треугольников сходственные стороны пропорциональны. Напротив равных углов в подобных треугольниках лежат сходственные стороны. Если считать LN=x. то EF=x-4. Составим и решим уравнение:
5/(х-4)=10/х
5х=10х-40
5х=40
х=8