
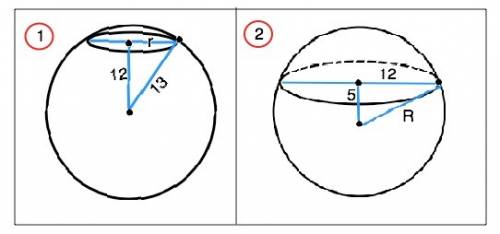
1. Всякая плоскость пересекает шар по окружности. Расстояние от центра шара до плоскости - длина перпендикулярного к ней отрезка. Следовательно, этот отрезок перпендикулярен и радиусу окружности, отсекаемой плоскостью. Расстояние от центра до плоскости и радиус r окружности - катеты прямоугольного треугольника, радиус R шара - его гипотенуза. По т.Пифагора r=√(13²-12²)=5 см. Длина окружности 2pr=10π см
2. Вершины треугольника, которые лежат в сфере, являются вершинами треугольника, вписанного в окружность, образованную плоскостью, проходящей на расстоянии 5 см от центра шара. Т.к. треугольник - прямоугольный, центр окружности лежит на середине гипотенузы. ⇒ r=24:2=12 см. Радиус r и расстояние от центра сферы до центра окружности сечения - катеты прямоугольного треугольника, радиус R сферы - его гипотенуза. R= √(5²+12²)=13 см
В прямоугольном треугольнике
синус острого угла - отношение противолежащего катета к гипотенузе
косинус острого угла - отношение прилежащего катета к гипотенузе
тангенс острого угла - отношение противолежащего катета к прилежащему (или синуса к косинусу)
cosA =AC/AB =sinB =1/2
Пусть AC=x, AB=2x
По теореме Пифагора
BC =√(AB^2 -AC^2) =x√(4-1) =x√3
tgA =BC/AC =√3
Или
cosA =cos(90-B) =sinB =1/2
sinA^2 +cosA^2 =1 => |:cosA^2
tgA^2 +1 =1/cosA^2 =>
tgA = +-√(1/cosA^2 -1) = +√(4-1) =√3
(тангенс острого угла положительный)