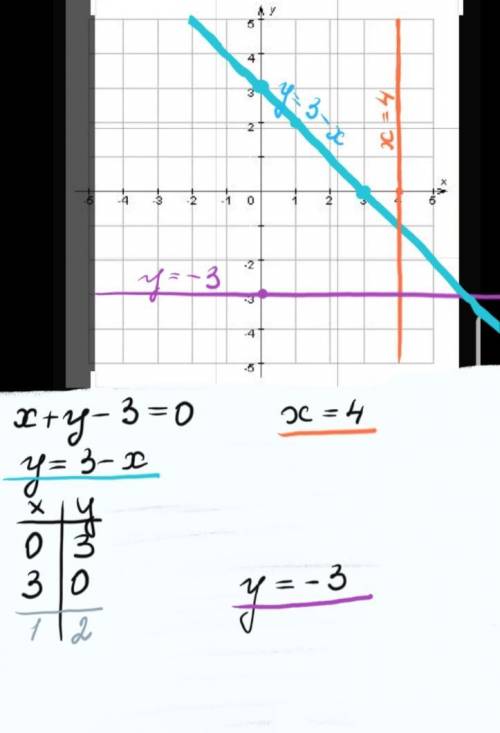
а)приведём х+у-3=0 к стандартному виду:
у=3-х
(подставим,вместо х числа и посчитаем у):
при х=0, у=3-0= 3
при х=3, у=3-3= 0
Отметим точки в системе координат и соединим в прямую линию.(рекомендую считать третью точку для себя,например х=1 ,у=2,т.к две точки всегда соединятся в прямую, а три могут не соединиться, тогда надо искать ошибку в расчётах).
б)х=4.
Отмечаем по х точку 4 и проводим прямую,параллельную оси ОУ.При любых значениях У, х =4.
в)у= -3
Отмечаем по у точку -3 и проводим прямую,параллельную оси ОХ.При любых значениях Х , у = -3.
SO=5√2см
S(∆SAC)=50см²
S(ABCD)=100см²
Объяснение:
Дано:
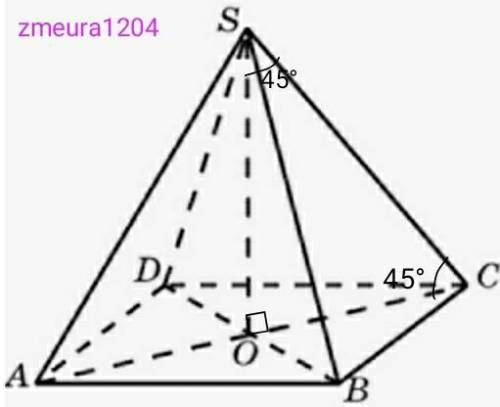
SABCD- пирамида.
ABCD- квадрат.
SC=SB=SA=SD=10см.
<SCO=45°
SO=?
S(∆SAC)=?
S(ABCD)=?
Решение
Рассмотрим треугольник ∆SOC
<SOC=90°; <SCO=45°; <OSC=45°.
Треугольник ∆SOC- прямоугольный, равнобедренный. SO=OC.
Пусть ОС будет х см, тогда SO тоже будет х см.
По теореме Пифагора SC²=SO²+OC², составляем уравнение.
х²+х²=10²
2х²=100
х=√50
х=5√2 см SO и ОС (высота пирамиды и половина диагонали квадрата).
SO=5√2 см.
АС=2*ОС=2*5√2=10√2 см.
S(∆SAC)=1/2*AC*SO=1/2*10√2*5√2=50см² площадь диагонального сечения.
AB=AC/√2=10√2/√2=10см сторона квадрата.
S(ABCD)=AB²=10²=100см²
RP+(RP+5).= 25. RP=10см, PK =15см.
RP+(RP-5).= 25 RP=15см, PK =10см.