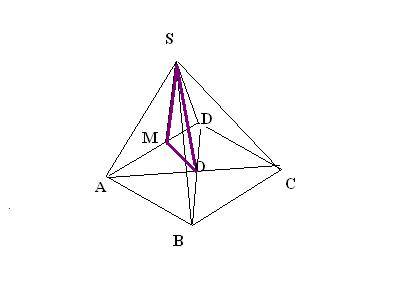
проведем в пирамиде диагонали основания и на их пересечении поставим точку О Диагональ квадрата со стороной 1 равна √2 половина диагонали √2/2
От точки О на сторону AD опустим перпендикуляр, из точки S сделаем тоже самое. Поставим точку М. Треугольник АDS равносторонний, поэтому перпендикуляр из вершины S на сторону AD тоже попадет в точку M
SO - высота правильной пирамиды равна половине диагонали основания.
SO=√2/2
SM - высота равностороннего треугольника ADS равна √3/2AD=√3/2
Треугольник МОS - прямоугольный угол О=90 градусов.
Косинус угла МS0 равен отношению прилежащего катета к гипотенузе
CosМS0=SO/SM=√(2/3)
sinMSO=корень(1-(√(2/3)^2)=1/√3
Вектор АС(-2;y-5;-8). Модуль вектора (его длина) |AC|=√(4+(y-5)²+64).
Вектор ВС(-6;(y-1);0). Модуль вектора (его длина) |BC|=√(36+(y-1)²+0).
Модули (длины) этих векторов равны по условию. Значит
√(4+(y-5)²+64)=√(36+(y-1)²+0).
Возведем обе части в квадрат:
4+(y-5)²+64=36+(y-1)² или
4+y²-10y+25+64=36+y²-2y+1
8y=56.
y=7.
ответ: С(0;7;0)
Проверим: |AC|=√(4+4+64)=√72, |BC|=√(36+36+0)=√72.
То есть точка С находится на равном расстоянии (равноудалена) от точек А и В.