Каждое боковое ребро составляет с плоскостью основания угол в 45° - следовательно, все ребра равны, а их проекции равны радиусу описанной около основания пирамиды окружности, Основание высоты пирамиды - центр О описанной окружности. . Величина её радиуса АО равна 2/3 высоты основания.
AH=AB•sin60°=4√3/2=2√3
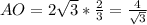
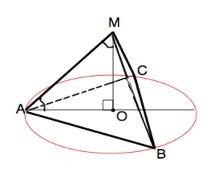
Высота МО перпендикулярна основанию
∆АМО - прямоугольный, острый угол МАО=45°, следовательно, второй АМО=45°, и высота пирамиды МО=АО=4/√3
Формула объёма пирамиды V=S•h:3
S(∆ABC)=AB²•√3/4=16√3/4=4√3
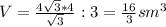
1) г
2)г
3)в
4)б
5)
Известно, что сумма углов выпуклого многоугольника равна 180(n-2), где n - число сторон многоугольника. ... 180(8-2)= 1080.Все углы правильного восьмиугольника равны, тогда каждый угол равен 1080/8=135 градусам. Внешний угол восьмиугольника является смежным с внутренним углом, он равен 180-135=45°
6)б