ответ: 0,8.
Объяснение:
Решение.
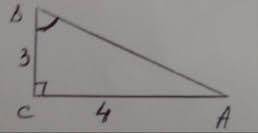
Отношение АС к АВ есть синус угла B.
sinB=AC/AB;
АВ находим по т. Пифагора:
АВ=√АС²+ВС²=√4²+3²=√16+9=√25=5 см.
sinB = 4/5 = 0,8.
Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.
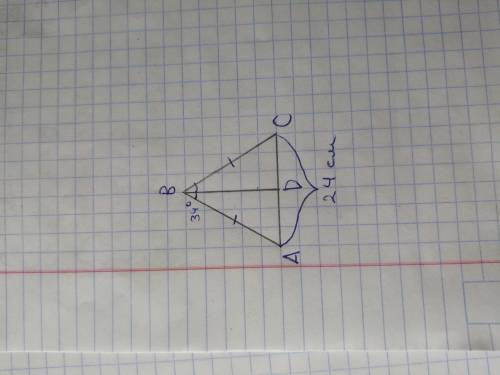
Дано: треугольник ABC - равнобедренный;
BD - биссектриса;
угол ABD = 34°;
AC = 24 см
Найти: угол B; угол BDC; сторону DC
1) ∠В = 2 × ∠ABD = 2 × 34° = 68°, т. к. BD - биссектриса делит Abc на равные углы.
2) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является высотой => BD⊥AC и ∠BDC = 90°.
3) треугольник ABC - равнобедренный => биссектриса, проведённая к основанию, является медианой => DC = 1/2 × AC = 1/2 × 25 = 12,5 см.
ответ: ∠В = 68°; ∠BDC = 90°; DC = 12,5 см.

Sin угла В = 4/5
Объяснение:
По теореме Пифагора находим гипотенузу :
АВ²= 9+16
АВ=5 см