ответ:8
Объяснение: введём обозначения: пусть большая наклонная c₁=17, её проекция а₁; меньшая наклонная с₂=10, её проекция а₂ ; расстояние от точки до плоскости обозначим b. 1)Тогда по условию а₁ - а₂ =9 , значит а₁=9 + а₂ 2)По теореме Пифагора из большего прямоугольного треугольника b²= 17²- (9+a₂)²=208-18a₂ -a₂² Из меньшего прямоугольного треугольника b²= 100-а₂². Левые части этих равенств равны, значит и правые равны 208-18a₂ -a₂² = 100 - а₂² 18a₂=108 а₂=6. Найдём b²= 100-а₂²=100-36=64 b=8
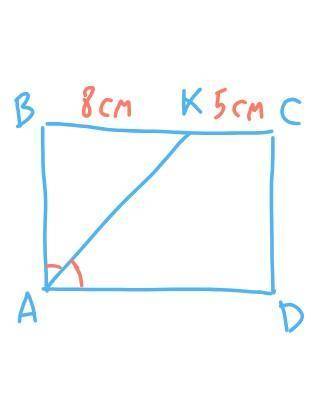
Периметр прямоугольника равен удвоенной сумме двух его смежных сторон. P = 2(AB+BC),
BC = BK + KC = 8 см + 5 см = 13 см.
AK — биссектрисса угла A, угол BAK = угол KAD = 90°÷2 = 45°,
Рассмотрим треугольник ABK. Сумма углов треугольника равна 180°. угол BKA = 180° – угол ABK – угол BAK = 180° – 90° – 45° = 45°, угол BKA = угол BAK, углы при основании равны, треугольник — равнобедренный, значит боковые стороны равны, AB = BK = 8см.
P = 2(AB + BC) = 2(8см + 13см) = 2 × 21 см = 42 см.
ответ: 42 см

6 см
Объяснение:
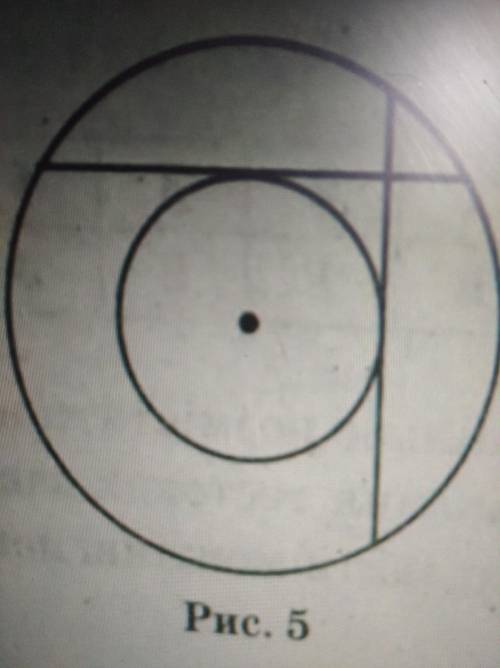
Радиусы OK и ОМ, проведённые в точки касания хорд с малой окружностью, будут перпендикулярны касательным - хордам АВ и CD. Но также, по свойству диаметра, перпендикулярного хорде, точки К и М будут лежать на серединах отрезков АВ и CD.
АВ=CD=AL+LB=16+4=20см
AK=KB=20/2=10см
KL=KB-LB=10-4=6см
KLMO - квадрат, поскольку все его смежные стороны имеют между собой прямой угол (2 - как радиусы к касательным, 1 - по условию перпендикулярности хорд, и оставшийся тоже получается 90°), и две его смежные стороны ОК и ОМ равны радиусу.
Значит ОМ=KL=6см